Đề thi lớp 1
Lớp 2Lớp 2 - kết nối tri thức
Lớp 2 - Chân trời sáng tạo
Lớp 2 - Cánh diều
Tài liệu tham khảo
Lớp 3Lớp 3 - liên kết tri thức
Lớp 3 - Chân trời sáng sủa tạo
Lớp 3 - Cánh diều
Tài liệu tham khảo
Lớp 4Sách giáo khoa
Sách/Vở bài bác tập
Đề thi
Lớp 5Sách giáo khoa
Sách/Vở bài tập
Đề thi
Lớp 6Lớp 6 - kết nối tri thức
Lớp 6 - Chân trời sáng sủa tạo
Lớp 6 - Cánh diều
Sách/Vở bài xích tập
Đề thi
Chuyên đề và Trắc nghiệm
Lớp 7Lớp 7 - kết nối tri thức
Lớp 7 - Chân trời sáng tạo
Lớp 7 - Cánh diều
Sách/Vở bài tập
Đề thi
Chuyên đề và Trắc nghiệm
Lớp 8Sách giáo khoa
Sách/Vở bài xích tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 9Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 10Lớp 10 - liên kết tri thức
Lớp 10 - Chân trời sáng sủa tạo
Lớp 10 - Cánh diều
Sách/Vở bài bác tập
Đề thi
Chuyên đề và Trắc nghiệm
Lớp 11Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề và Trắc nghiệm
Lớp 12Sách giáo khoa
Sách/Vở bài bác tập
Đề thi
Chuyên đề & Trắc nghiệm
ITNgữ pháp giờ Anh
Lập trình Java
Phát triển web
Lập trình C, C++, Python
Cơ sở dữ liệu

Công thức, Định nghĩa Toán, Lí, Hóa
Đường thẳng
Hình tam giác
Các trường phù hợp tam giác bằng nhau
Hình thang
Hình bình hành
Hình thoi
Hình chữ nhật
Tổng hợp kiến thức và kỹ năng cơ bạn dạng Toán lớp 5 học kì 1, học tập kì 2 chi tiết
Tải xuống
ÔN TẬP VÀ BỔ SUNG VỀ PHÂN SÔ
1. Các tính chất cơ bạn dạng của phân số
*) ví như nhân cả tử số và mẫu số của một phân số cùng với cùng một vài tự nhiên khác thì được một phân số bởi phân số đang cho.
Bạn đang xem: Kiến thức toán lớp 5
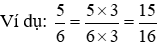
*) Nếu phân tách cả tử số và mẫu mã số của một phân số cùng với cùng một trong những tự nhiên khác thì được một phân số bằng phân số vẫn cho.
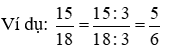
2. Rút gọn gàng phân số
Phương pháp:
+ Xét coi tử số và chủng loại số cùng phân tách hết mang lại số tự nhiên nào lớn hơn 1.
+ chia tử số và mẫu mã số đến số đó.
+ Cứ làm cho như thế cho đến khi nhận thấy phân số về tối giản.
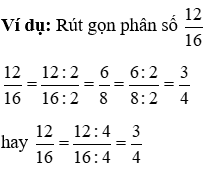
3. Quy đồng chủng loại số của các phân số
Phương pháp:
+ Lấy tử số và mẫu mã số của phân số trước tiên nhân với mẫu mã số của phân số thiết bị hai.
+ Lấy tử số và mẫu số của phân số trang bị hai nhân với chủng loại số của phân số sản phẩm công nghệ nhất.

4. đối chiếu hai phân số
4.1. So sánh hai phân số cùng chủng loại số
Trong nhì phân số cùng chủng loại số:
· Phân số nào bao gồm tử số bé nhiều hơn thì bé bỏng hơn.
· Phân số nào bao gồm tử số lớn hơn nữa thì lớn hơn.
· trường hợp tử số bằng nhau thì hai phân số đó bởi nhau.
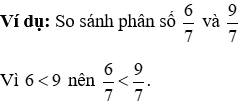
4.2. So sánh hai phân số không cùng mẫu số
Muốn so sánh hai phân số khác mẫu số, ta hoàn toàn có thể quy đồng chủng loại số nhì phân số đó, rồi so sánh các tử số của nhị phân số mới.
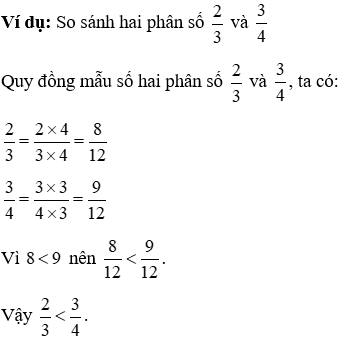
5. Phân số thập phân
Khái niệm: các phân số bao gồm mẫu số là được hotline là phân số thập phân
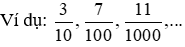
6. Phép cộng và trừ nhị phân số có cùng mẫu số
Phương pháp: mong mỏi cộng (hoặc trừ) nhị phân số cùng mẫu mã số ta cộng (hoặc trừ) nhì tử số cùng nhau và không thay đổi mẫu số.

7. Phép cùng và trừ nhì phân số không cùng mẫu số
Phương pháp: ước ao cộng (hoặc trừ) nhì phân số khác mẫu số ta quy đồng mẫu mã số, rồi cùng (hoặc trừ) nhì phân số sẽ quy đồng mẫu số.

8. Phép nhân cùng phép chia hai phân số
● mong muốn nhân hai phân số ta lấy tử số nhân cùng với tử số, mẫu số nhân với mẫu số.
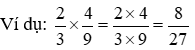
● ý muốn chia nhì phân số cho một phân số ta mang phân số đầu tiên nhân cùng với phân số sản phẩm hai hòn đảo ngược.
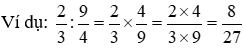
HỖN SỐ
1. Khái niệm hỗn số
Hỗn số có hai yếu tố là phân nguyên với phần phân số.
Ví dụ: lếu láo số
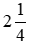
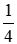
Chú ý: Phần phân số của lếu số khi nào cũng nhỏ dại hơn
2. Giải pháp chuyển láo số thành phân số
Phương pháp:
+ Tử số bởi phần tại sao với chủng loại số rồi cộng với tử số tại vị trí phân số.
+ mẫu mã số bởi mẫu số tại đoạn phân số.

3. Bí quyết chuyển phân số thành láo lếu số
Phương pháp:
+ Tính phép chia tử số mang lại mẫu số
+ không thay đổi mẫu số của phần phân số; Tử số ngay số dư của phép phân chia tử số đến mẫu số
+ Phần nguyên bởi thương của phép phân chia tử số đến mẫu số

4. Những phép toán với láo số
4.1. Phép cộng, trừ láo lếu số
Cách 1. Chuyển hỗn số về phân số
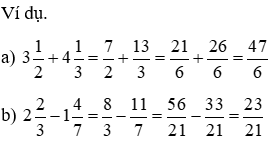
Cách 2. Bóc tách hỗn số nguyên tố nguyên và phần phân số
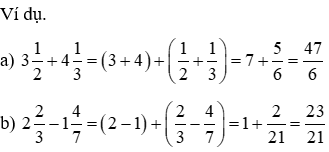
4.2. Phép nhân, chia hỗn số
Phương pháp: ao ước nhân (hoặc chia) nhị hỗn số, ta đưa hai hỗn số về dạng phân số rồi nhân (hoặc chia) nhì phân số vừa chuyển đổi.
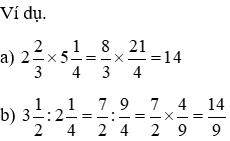
5. đối chiếu hỗn số
Cách 1. Chuyển hỗn số về phân số
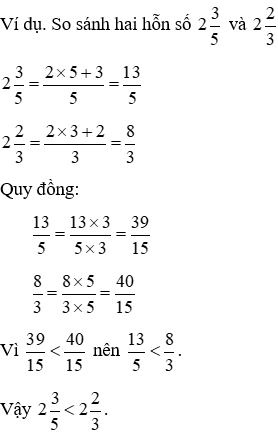
Cách 2. đối chiếu phần nguyên với phần phân số

SỐ THẬP PHÂN VÀ CÁC PHÉP TÍNH VỚI SỐ THẬP PHÂN
1. Tư tưởng số thập phân
Ôn lại phân số thập phân: các phân số có mẫu số là ,… được hotline là phân số thập phân.
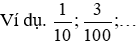
Mỗi số thập phân tất cả hai phần: Phần nguyên và phần thập phân (chúng được ngăn cách bởi lốt phẩy)
Ví dụ. Số thập phân 4,35 có hai phần: Phần nguyên (4) cùng phần thập phân (35)
2. Chuyển các phân số thành số thập phân
Phương pháp: giả dụ phân số đã mang đến chưa là phân số thập phân thì ta chuyển những phân số thành phân số thập phân rồi đưa thành số thập phân.
Ví dụ. Chuyển những phân số sau thành phân số thập phân:

3. Nhảy số thập phân thành phân số
Phương pháp: Viết số thập phân bên dưới dạng phân số thập phân kế tiếp thực hiện các bước rút gọn gàng phân số thập phân đó.
(1, 2, 3 chữ số phần thập phân khi đưa sang phân số thập phân gồm mẫu số là 10, 100, 100,…)
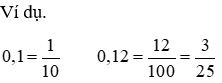
4. Viết các số đo độ dài, khối lượng… bên dưới dạng số thập phân
Phương pháp:
- search mối liên hệ giữa hai đơn vị đo vẫn cho.
- chuyển số đo độ dài đã cho thành phân số thập phân có đơn vị đo mập hơn.
- gửi từ số đo độ nhiều năm dưới dạng phân số thập tạo thành số đo độ dài tương ứng dưới dạng số thập phân có đơn vị lớn hơn.
Ví dụ. Viết số đo dưới dạng phân số thập phân và số thập phân
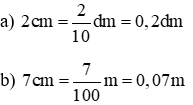
5. Viết lếu láo số thành phân số thập phân
Phương pháp: Đổi láo số về dạng phân số thập phân, kế tiếp chuyển thành số thập phân
Ví dụ. Viết láo lếu số thành số thập phân:
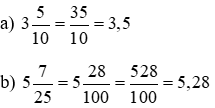
6. Phép cộng và phép trừ những số thập phân
6.1. Phép cộng hai số thập phân
Muốn cùng hai số thập phân ta làm cho như sau:
- Viết số hạng này dưới số hạng kia sao cho các chữ số ở và một hàng để thẳng cột cùng với nhau.
- cộng như cộng những số từ bỏ nhiên.
- Viết vết phẩy sống tổng trực tiếp cột với những dấu phẩy của các số hạng.
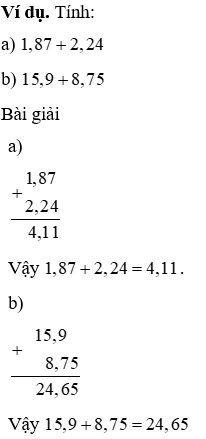
6.2. Phép trừ nhị số thập phân
Muốn trừ một vài thập phân cho một số thập phân ta làm như sau:
- Viết số trừ bên dưới số bị trừ thế nào cho các chữ số ở và một hàng đặt thẳng cột nhau.
- thực hiện phép trừ như trừ những số trường đoản cú nhiên.
- Viết lốt phẩy sống hiệu thẳng cột với các dấu phẩy của số bị trừ và số trừ.

6.3. Phép nhân những số thập phân
a) Nhân một vài thập phân với một số trong những tự nhiên
Muốn nhân một trong những thập phân với một số trong những tự nhiên ta là như sau:
+ Nhân như nhân những số tự nhiên
+ Đếm xem vào phần thập phân của số thập phân có bao nhiêu chữ số rồi sử dụng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.

b) Nhân một vài thập phân cùng với 10, 100, 1000,…
Muốn nhân một trong những thập phân cùng với 10, 100, 100,… ta chỉ bài toán chuyển lốt phẩy của số đó lần lượt quý phái bên đề xuất một, hai, ba,… chữ số.
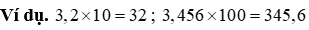
c) Nhân một số thập phân với một số trong những thập phân
Muốn nhân một trong những thập phân với một trong những thập phân ta có tác dụng như sau:
+ triển khai phép nhân như nhân các số từ bỏ nhiên
+ Đếm xem vào phần thập phân của cả hai thừa số có bao nhiêu chữ số rồi sử dụng dấu phẩy bóc ở tích ra bấy nhiêu chữ số tính từ lúc phải sang trái

(hai quá số có tất cả ba chữ số ở trong phần thập phân, ta sử dụng dấu phẩy tách ở tích ra tía chữ số kể từ trái thanh lịch phải)
d) Nhân một vài thập phân với 0,1; 0,01; 0,001;…
Muốn nhân một số trong những thập phân cùng với 0,1; 0,01; 0,001;… ta chỉ việc chuyển dấu phẩy của số kia lần lượt sang bên trái một, hai, ba,… chữ số.
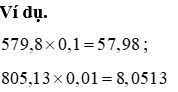
6.4. đặc thù của phép nhân

6.5. Phép chia những số thập phân
a) Chia một số trong những thập phân cho một số trong những tự nhiên
Muốn chia một vài thập phân cho một trong những tự nhiên ta có tác dụng như sau:
- chia phần nguyên của số bị chia cho số chia.
- Viết dấu phẩy vào bên đề nghị thương đã tìm kiếm được trước khi rước chữ số đầu tiên ở phần thập phân của số bị phân chia đẻ triển khai phép chia.
- thường xuyên chia với từng chữ số thập phân của số bị chia.
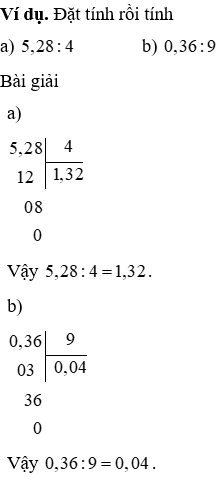
b) Chia một vài thập phân đến 10, 100, 1000,…
Muốn chia một vài thập phân cho 10, 100, 1000,… ta chỉ việc chuyển vết phẩy của số kia lần lượt sang phía trái một, hai, ba,… chữ số.
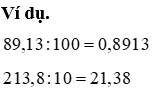
c) Chia một trong những tự nhiên cho một vài tự nhiên nhưng mà thương tìm được là một trong những thập phân
Khi chia một trong những tự nhiên cho một số trong những tự nhiên bên cạnh đó dư, ta thường xuyên chia như sau:
+ Viết vết phẩy vào bên nên số thương.
+ hiểu biết thêm vào bên đề nghị số dư một chữ số 0 rồi phân chia tiếp.
+ ví như còn dư nữa, ta lại viết chế tạo bên yêu cầu số dư new một chữ số 0 rồi tiếp tục chia, và có thể cứ làm như thế mãi.
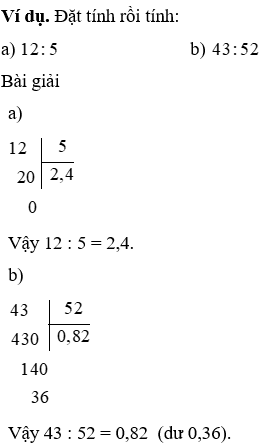
d) Chia một số trong những tự nhiên cho một vài thập phân
Muốn chia một số trong những tự nhiên cho một trong những thập phân ta có tác dụng như sau:
- Đếm xem có bao nhiêu chữ số tại đoạn thập phân của số phân chia thì viết cung ứng bên buộc phải số bị chia từng ấy chữ số 0.
- vứt dấu phẩy nghỉ ngơi số phân tách rồi triển khai phép phân chia như chia những số trường đoản cú nhiên.

e) Chia một số thập phân cho 0,1; 0,01; 0,001…
Muốn chia một vài thập phân đến 0,1; 0,01; 0,001… ta chỉ vấn đề chuyển lốt phẩy của số kia lần lượt quý phái bên đề xuất một, hai, ba,… chữ số.

f) Chia một vài thập phân cho một trong những thập phân
Muốn chia một số trong những thập phân cho một thập phân ta có tác dụng như sau:
+ Đếm xem có bao nhiêu chữ số tại vị trí thập phân của số phân chia thì chuyển dấu phẩy nghỉ ngơi số bị chia sang bên đề xuất bấy nhiêu chữ số.
+ bỏ dấu phẩy làm việc số phân tách rồi tiến hành phép phân chia như phân tách cho số từ bỏ nhiên.

TỈ SỐ PHẦN TRĂM
1. Quan niệm Tỉ số phần trăm
có thể viết dưới dạng là a%, giỏi = a%
+ Tỉ số phần trăm là tỉ số của nhì số mà trong các số đó ta đưa mẫu mã của tỉ số về 100.
+ Tỉ số tỷ lệ thường được dùng để biểu thị độ lớn kha khá của một lượng này so với lượng khác.
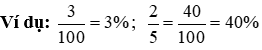
2. Các phép tính với tỉ số phần trăm

3. Các bài toán cơ bạn dạng của tỉ số phần trăm
Bài toán 1: tìm kiếm tỉ số tỷ lệ của nhị số
Muốn tìm kiếm tỉ số tỷ lệ của nhị số ta làm như sau:
- tìm kiếm thương của hai số kia dưới dạng số thập phân.
- Nhân thương đó với 100 và viết thêm kí hiệu tỷ lệ (%) vào bên đề xuất tích tra cứu được
Ví dụ: tìm kiếm tỉ số xác suất của 315 với 600

Bài toán 2: Tìm giá chỉ trị tỷ lệ của một trong những cho trước
Muốn tìm cực hiếm phần của một số trong những cho trước ta mang số đó phân chia cho 100 rồi nhân cùng với số xác suất hoặc đem số đó nhân cùng với số tỷ lệ rồi phân chia cho 100.
Ví dụ. trường Đại Từ có 600 học sinh. Số học viên nữ chiếm 45% số học viên toàn trường. Tính số học viên nữ của trường.

Bài toán 3: tra cứu một số, biết quý hiếm một tỉ số xác suất của số đó
Muốn tìm một số trong những khi biết giá chỉ trị xác suất của số đó ta mang giá trị xác suất của số đó chia cho số xác suất rồi nhân với 100 hoặc ta lấy giá trị xác suất của số đó nhân với 100 rồi chia cho số phần trăm.
Ví dụ. Tìm một trong những biết 30% của nó bằng 72.

ĐẠI LƯỢNG VÀ ĐO ĐẠI LƯỢNG
1. Bảng đơn vị chức năng đo độ dài
Lớn hơn mét | Mét | Bé rộng mét | ||||
km | hm | dam | m | dm | cm | mm |
1km | 1hm | 1dam | 1m | 1dm | 1cm | 1mm |
= 10hm | = 10dam | = 10m | = 10 dm | = 10cm | = 10mm | |
= km | = hm | = dam | = m | = dm | = mm | |
= 0,1km | = 0,1hm | = 0,1dam | = 0,1m | = 0,1dm | = 0,1mm |
Nhận xét
- Hai đơn vị chức năng đo độ nhiều năm liền nhau gấp ( hoặc kém) nhau 10 lần.

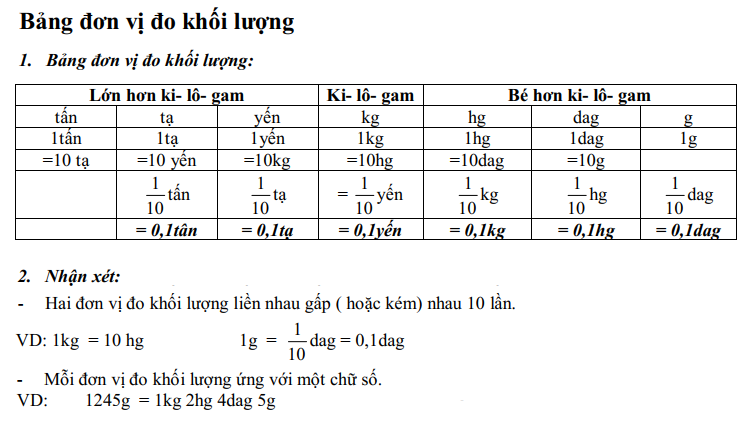
2. Bảng đơn vị đo khối lượng
Lớn hơn ki-lô- gam | Ki-lô- gam | Bé hơn ki-lô- gam | ||||
tấn | tạ | yến | kg | hg | dag | g |
1tấn | 1tạ | 1yến | 1kg | 1hg | 1dag | 1g |
=10 tạ | =10 yến | =10kg | =10hg | =10dag | =10g | |
= tấn | = tạ | = yến | = kg | = hg | = dag | |
= 0,1tân | = 0,1tạ | = 0,1yến | = 0,1kg | = 0,1hg | = 0,1dag |
Nhận xét:
- Hai đơn vị chức năng đo trọng lượng liền nhau vội (hoặc kém) nhau 10 lần.
- Mỗi đơn vị đo khối lượng ứng với một chữ số.
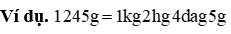
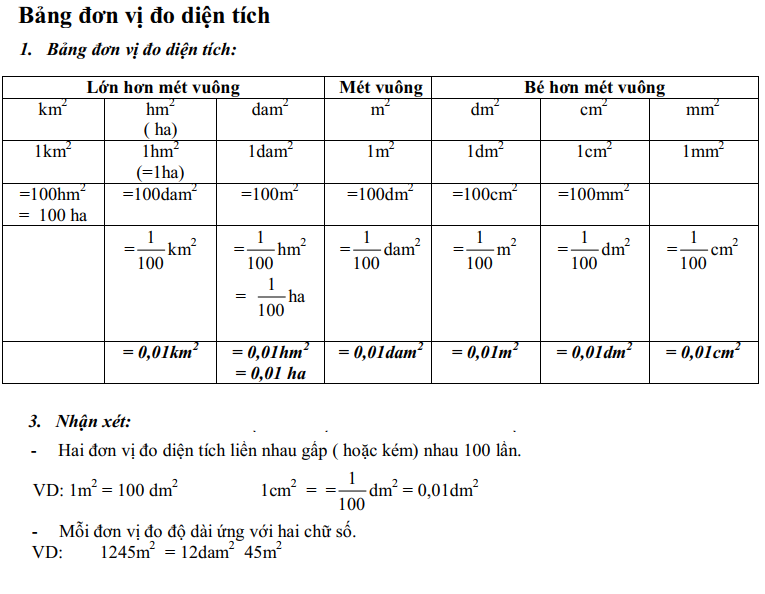
3. Bảng đơn vị chức năng đo diện tích s
Lớn rộng mét vuông | Mét vuông | Bé rộng mét vuông | |||||
km2 | hm2 (ha) | dam2 | m2 | dm2 | cm2 | mm2 | |
1km2 | 1hm2 (=1ha) | 1dam2 | 1m2 | 1dm2 | 1cm2 | 1mm2 | |
= 100hm2 = 100 ha | = 100dam2 | = 100m2 | = 100dm2 | = 100cm2 | =100mm2 | ||
= km2 | = hm2 = ha | = dam2 | = m2 | = dm2 | = cm2 | ||
= 0,01km2 | = 0,01hm2 = 0,01 ha | = 0,01dam2 | = 0,01m2 | = 0,01dm2 | = 0,01cm2 |
Nhận xét:
- Hai đơn vị đo diện tích liền nhau vội (hoặc kém) nhau 100 lần.

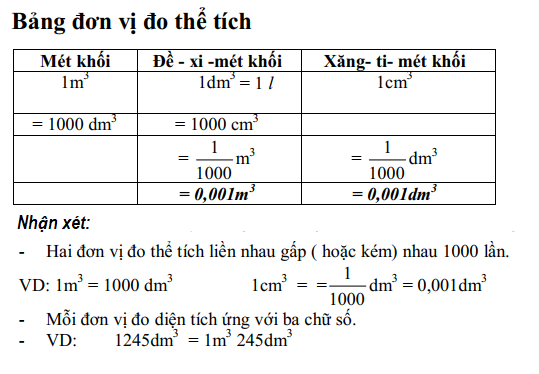
4. Bảng đơn vị chức năng đo thể tích
Mét khối | Đề - xi -mét khối | Xăng- ti- mét khối |
1m3 | 1dm3 | 1cm3 |
= 1000 dm3 | = 1000 cm3 | |
= m3 | = dm3 | |
= 0,001m3 | = 0,001dm3 |
Nhận xét:
- Hai đơn vị đo thể tích ngay lập tức nhau gấp (hoặc kém) nhau 1000 lần.

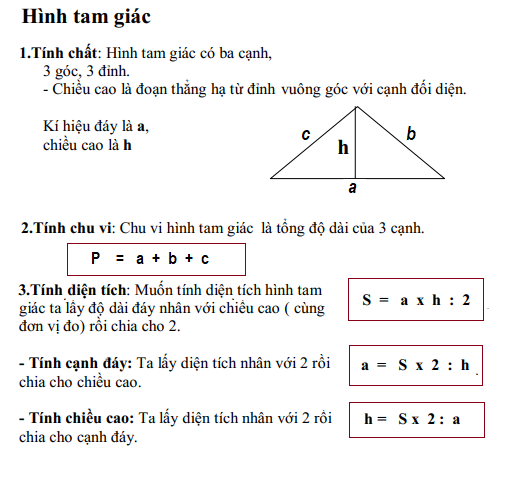
HÌNH TAM GIÁC
1. Hình tam giác
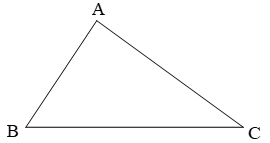
Hình tam giác ABC có:
- Ba cạnh là: cạnh AB, cạnh AC, cạnh BC.
- tía đỉnh là: đỉnh A, đỉnh B, đỉnh C.
- Ba góc là:
Góc đỉnh A, cạnh AB và AC (gọi tắt là góc A);
Góc đỉnh B, cạnh cha và BC (gọi tắt là góc B);
Góc đỉnh C, cạnh AC với CB (gọi tắt là góc C).
Vậy hình tam giác bao gồm 3 cạnh, 3 góc, 3 đỉnh.
2. Một số mô hình tam giác
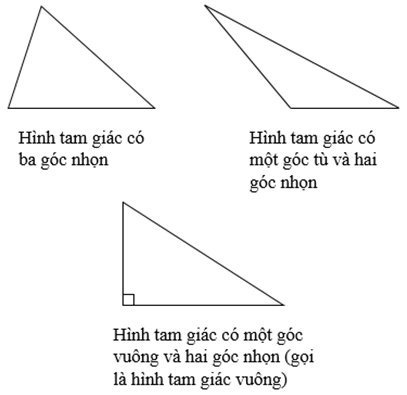
Có 3 mô hình tam giác:
- Hình tam giác có ba góc nhọn
- Hình tam giác gồm một góc tù và hai góc nhọn
- Hình tam giác gồm một góc vuông và hai góc nhọn (gọi là hình tam giác vuông)
*) hình vẽ minh họa
3. Cách xác định đáy và mặt đường cao của hình tam giác
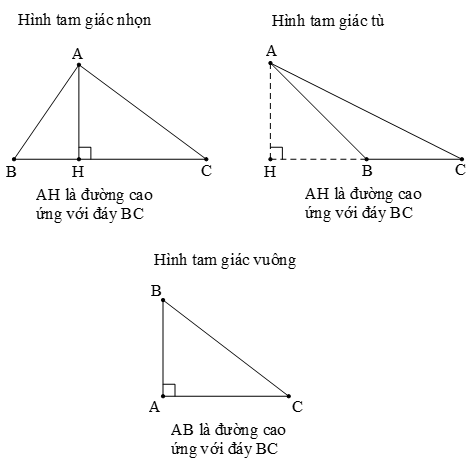
4. Diện tích s hình tam giác
Quy tắc: ước ao tính diện tích s hình tam giác ta đem độ lâu năm đáy nhân với chiều cao (cùng một đơn vị chức năng đo) rồi phân chia cho 2.
Xem thêm: Giải bóng đá anh : lịch thi đấu, trực tiếp, video bàn thắng mới nhất
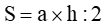
Ví dụ. Tính diện tích hình tam giác bao gồm độ nhiều năm đáy là 13cm và độ cao là 4cm.

HÌNH THANG
1. Định nghĩa: Hình thang gồm một cặp cạnh đối diện tuy nhiên song.
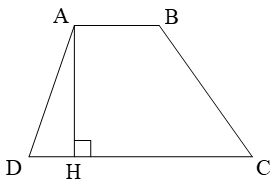
Hình thang ABCD có:
● Cạnh lòng AB cùng cạnh lòng DC. Sát bên AD và sát bên BC.
● AB song song cùng với DC.
● AH là đường cao, độ lâu năm AH là độ cao
*) Hình thang vuông:
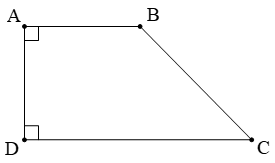
AD vuông góc cùng với hai lòng AB, DC.
AD là con đường cao của hình thang của ABCD.
2. Diện tích s hình thang: muốn tính diện tích s hình thang ta mang tổng độ nhiều năm hai lòng nhân với độ cao (cùng đơn vị đo) rồi phân chia cho 2.
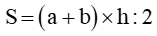
Trong đó:
● a là đáy nhỏ
● b là đáy lớn
● h là chiều cao
Ví dụ. Tính diện tích s hình thang biết độ nhiều năm hai lòng lần lượt là , và chiều cao .

HÌNH TRÒN
1. Hình tròn. Đường tròn.
Vẽ con đường tròn vai trung phong O, các điểm A, điểm B, điểm M, điểm C nằm trê tuyến phố tròn.
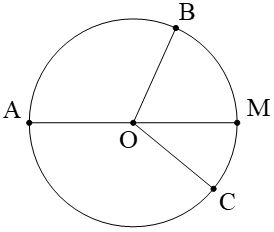
*) chào bán kính
- Nối vai trung phong O với cùng 1 điểm A trên phố tròn. Đoạn trực tiếp OA là bán kính của con đường tròn. Tất cả các nửa đường kính của hình tròn đều đều nhau OA = OB = OC = OM.
- nửa đường kính được kí hiệu là r.
*) Đường kính
Đoạn trực tiếp AM nối hai điểm M, N của đường tròn và trải qua tâm O là 2 lần bán kính của hình tròn.
Đường kính được kí hiệu là
Trong một hình tròn, 2 lần bán kính dài gấp hai lần bán kính (d = 2r)
*) hình tròn trụ là hình gồm các điểm nằm trên tuyến đường tròn và các điểm nằm bên trong hình tròn đó.
2. Chu vi hình tròn
*) mong tính chu vi hình tròn ta lấy 2 lần bán kính nhân với 3,14:
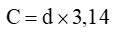
(C là chu vi hình tròn, d là 2 lần bán kính hình tròn)
Ví dụ. Tính chu vi hình tròn có 2 lần bán kính là 8cm

*) hy vọng tính chu vi hình tròn ta lấy 2 lần nửa đường kính nhân cùng với 3,14.
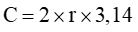
Ví dụ. Tính chu vi hình tròn trụ có bán kính là

3. Diện tích hình tròn
Muốn tính diện tích s của hình trụ ta lấy nửa đường kính nhân với nửa đường kính rồi nhân cùng với 3,14.
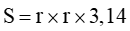
(S là diện tích s hình tròn, r là nửa đường kính hình tròn)
Ví dụ. Tính diện tích hình tròn trụ có cung cấp kính

HÌNH HỘP CHỮ NHẬT
1. Định nghĩa
Hình vỏ hộp chữ nhật là một hình không khí có 6 mặt đa số là hình chữ nhật.
Hai mặt đối lập nhau của hình chữ nhật được xem là hai dưới mặt đáy của hình chữ nhật. Những mặt còn lại đều là mặt mặt của hình chữ nhật.
Hình hộp chữ nhật tía chiều: chiều dài, chiều rộng, chiều cao
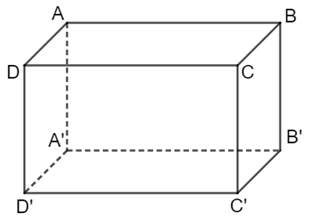
Hình hộp chữ nhật có:
+ 12 cạnh: AB, BC, CD, DA, A’B’, B’C’, C’D’, D’A’, AA’, BB’, CC’, DD’
+ 8 đỉnh: đỉnh A, đỉnh B, đỉnh C, đỉnh D, đỉnh A’, đỉnh B’, đỉnh C, đỉnh D’
+ 6 mặt: ABCD, BCC’B’, A’B’C’D’, DCD’C’, ADD’C’, ABB’A’.
2. Công thức
Cho hình vẽ:
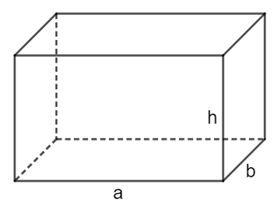
Trong đó:
● a: Chiều dài
● b: Chiều rộng
● h: Chiều cao
2.1. Phương pháp tính diện tích s xung xung quanh hình hộp chữ nhật
Diện tích bao phủ hình vỏ hộp chữ nhật bởi tích của chu vi đáy và chiều cao:
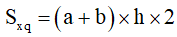
Ví dụ: Tính diện tích xung quanh của hình vỏ hộp chữ nhật, biết chiều dài đôi mươi m, chiều rộng lớn 7 m, độ cao 10 m.

2.2. Phương pháp tính diện tích toàn phần hình vỏ hộp chữ nhật
Diện tích toàn phần hình hộp chữ nhật bởi tổng diện tích s xung quanh hình vỏ hộp chữ nhật và diện tích nhì mặt còn lại.
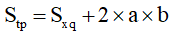
Ví dụ: một chiếc thùng hình chữ nhật có chiều cao là 3 cm, chiều lâu năm là 5,4 cm, chiều rộng lớn là 2 cm. Tính diện tích toàn phần của loại thùng đó.

2.3. Phương pháp tính thể tích hình hộp chữ nhật
Thể tích của hình vỏ hộp chữ nhật bởi tích của diện tích s đáy và chiều cao.
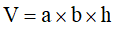
Ví dụ: Tính thể tích hình vỏ hộp chữ nhật tất cả chiều dài 9cm, chiều rộng lớn 5cm và độ cao .

HÌNH LẬP PHƯƠNG
1. Định nghĩa
Hình lập phương là hình khối bao gồm chiều rộng, chiều nhiều năm và chiều cao đều bởi nhau.
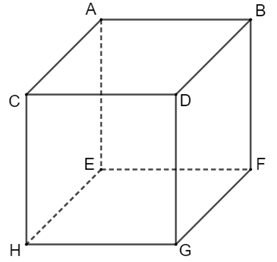
Hình lập phương có:
+ 8 đỉnh: đỉnh A, đỉnh C, đỉnh B, đỉnh D, đỉnh E, đỉnh F, đỉnh G, đỉnh H
+ 12 cạnh bởi nhau: AB = BD = DC = CA = CH = AE = DG = BF = FG = sắt = EH = HG
+ 6 phương diện là hình vuông vắn bằng nhau
2. Công thức
Cho hình vẽ:
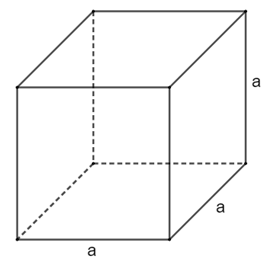
Trong đó: a là độ lâu năm cạnh của hình lập phương
2.1. Phương pháp tính diện tích xung xung quanh hình lập phương
Diện tích bao quanh của hình lập phương bằng diện tích một khía cạnh nhân cùng với 4.
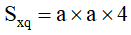
Ví dụ: Tính diện tích s xung xung quanh của hình lập phương gồm cạnh 6cm.

2.2. Phương pháp tính diện tích s toàn phần hình lập phương
Diện tích toàn phần của hình lập phương bằng diện tích s một mặt nhân cùng với 6.
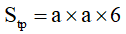
Ví dụ: Tính diện tích s toàn phần của hình lập phương có cạnh 5cm.

2.3. Cách làm tính thể tích hình lập phương
Muốn tính thể tích hình lập phương ta đem cạnh nhân cùng với cạnh nhân rồi nhân cùng với cạnh.
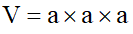
Ví dụ: Tính thể tích lập phương gồm cạnh 3cm.

SỐ ĐO THỜI GIAN – CHUYỂN ĐỘNG ĐỀU
1. Bảng đơn vị đo thời gian
Các đơn vị đo thời gian
1 gắng kỉ = 100 năm 1 năm = 12 tháng 1 năm = 365 ngày 1 năm nhuận = 366 ngày Cứ 4 năm lại có 1 năm nhuận | 1 tuần lễ = 7 ngày 1 ngày = 24 giờ 1 giờ đồng hồ = 60 phút 1 phút = 60 giây |
Tháng 1, 3, 5, 7, 8, 10, 12 tất cả 31 ngày.
Tháng 4, 6, 9, 11 gồm 30 ngày.
Tháng 2 có 28 ngày (vào năm nhuận gồm 29 ngày)
Ví dụ:
+) 1 năm rưỡi = 1,5 năm = 12 tháng × 1,5 = 1,8 tháng
+)
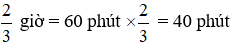
+) 0,5 giờ đồng hồ = 60 phút × 0,5 = 30 phút
+) 216 phút = 3 giờ 36 phút = 3,6 tiếng (thực hiện nay phép phân tách 216 đến 60)
2. Phép toán cùng với số đo thời gian
a) cộng số đo thời gian
Phương pháp:
- Đặt tính thẳng hàng và thực hiện tính như so với phép cộng các số từ nhiên.
- lúc tính sau mỗi tác dụng ta buộc phải ghi đơn vị chức năng đo tương ứng.
- trường hợp số đo thời gian ở đơn vị nhỏ xíu có thể biến hóa sang đơn vị chức năng lớn thì ta thực hiện chuyển đổi sang đơn vị chức năng lớn hơn.
Ví dụ. Đặt tính rồi tính:
a) 2 giờ 15 phút + 4 tiếng 22 phút
b) 5 phút 38 giây + 3 phút 44 giây
Bài giải
a)
Vậy 2 tiếng 15 phút + 4 giờ 22 phút = 6 tiếng 37 phút
b)
Vậy 5 tiếng 38 giây + 3h 44 giây = 9 phút 22 giây
b) Trừ số đo thời gian
Phương pháp:
- Đặt tính thẳng hàng và tiến hành tính như so với phép trừ những số tự nhiên.
- khi tính sau mỗi kết quả ta đề nghị ghi đơn vị chức năng đo tương ứng.
- ví như số đo theo đơn vị nào đó ở số bị trừ nhỏ nhiều hơn số đo tương ứng ở số trừ thì cần đổi khác 1 đơn vị hàng lớn hơn liền kề sang solo vị nhỏ dại hơn rồi triển khai phép trừ như bình thường.
Ví dụ. Đặt tính rồi tính:
a) 9h 45 phút – 3h 12 phút
b) 14 phút 15 giây – 8 phút 39 giây
Bài giải

c) Nhân số đo thời gian
Phương pháp:
- Đặt tính thẳng hàng và thực hiện tính như đối với phép nhân các số từ nhiên.
- khi tính sau mỗi công dụng ta đề xuất ghi đơn vị chức năng đo tương ứng.
- giả dụ số đo thời hạn ở đối chọi vị bé nhỏ ta bao gồm thể biến hóa sang đơn vị lớn thì ta thực hiện biến đổi sang đơn vị lớn hơn.
Ví dụ. Đặt tính rồi tính:
a) 3h 12 phút × 3
b) 5 năm 9 tháng × 2
Bài giải

Vậy 5 năm 9 mon × 2 = 11 năm 6 tháng.
TOÁN CHUYỂN ĐỘNG ĐỀU
1. Vận tốc: mong tính gia tốc ta mang quãng đường phân tách cho thời gian.
v = s : t
2. Quãng đường: muốn tính quãng đường ta lấy vận tốc nhân với thời gian.
s = v × t
3. Thời gian: mong mỏi tính thời gian ta mang quãng đường phân chia cho vận tốc
t = s : v
Hai vận động ngược chiều chạm mặt nhau

Ví dụ. và một lúc, ô tô đi từ bỏ A mang đến B với gia tốc là 50km/giờ với xe thứ đi trường đoản cú B đến A với gia tốc là 36km/giờ. Biết độ dài quãng mặt đường AB là 215km. Hỏi tính từ lúc lúc bắt đầu đi, sau mấy giờ nhị xe đó chạm mặt nhau?
Bài giải
Tổng gia tốc của nhì xe là:
50 + 36 = 86 (km/giờ)
Thời gian đi để hai xe gặp mặt nhau là:
215 : 86 = 2,5 (giờ)
Đáp số: 2,5 giờ
Hai chuyển động cùng chiều chạm mặt nhau

Ví dụ. và một lúc, xe hơi đi từ A mang lại B với tốc độ 50km/giờ đuổi theo một xe sản phẩm đi trường đoản cú B đến C với gia tốc là 38km/giờ. Biết độ nhiều năm quãng đường AB là 18km. Hỏi kể từ lúc bắt đầu đi, sau mấy tiếng ô tô đuổi kịp xe máy?
Bài giải
Hiệu tốc độ của hai xe là:
50 – 38 = 12 (km/giờ)
Thời gian đi nhằm ô tô đuổi theo kịp xe lắp thêm là:
18 : 12 = 1,5 (giờ)
Đáp số: 1,5 giờ
Chuyển hễ trên cái nước
*) một số kiến thức đề nghị nhớ
Vận tốc thực của thuyền = (vận tốc xuôi loại + vận tốc ngược dòng) : 2
Vận tốc làn nước = (vận tốc xuôi mẫu – tốc độ ngược dòng) : 2
Vận tốc xuôi dòng – gia tốc ngược loại = gia tốc dòng nước × 2
* Chú ý
Vận tốc thực của thuyền đó là vận tốc của thuyền khi làn nước đứng im (hay làn nước yên lặng).
Trên và một quãng đường thì tốc độ và thời hạn là nhì đại lượng tỉ trọng nghịch.
Ví dụ. tốc độ ca nô lúc nước im là 25km/giờ. Vận tốc dòng nước là 3km/giờ. Tính:
a) vận tốc của ca nô khi đi xuôi dòng.
b) vận tốc của ca nô khi đi ngược dòng
Bài giải
a) tốc độ của ca nô khi đi xuôi dòng là:
25 + 3 = 28 (km/giờ)
b) gia tốc của ca nô lúc đi ngược mẫu là:
25 – 3 = 22 (km/giờ)
Đáp số:
a) 28 km/giờ
b) 22 km/giờ
Tải xuống
Bài viết này đang giúp các bạn và những em tổng hợp cục bộ chương trình Toán Lớp 5, mức độ trung bình – khá, yêu cầu các em sau khi học dứt lớp 5 ít nhất là hoàn toàn có thể nắm được tổng thể kiến thức liệt kê trong bài viết này. Để học thêm về các phần nâng cao của chương trình toán lớp 5 tuyệt hướng dẫn giải các bài toán vào ngôi trường chuyên, đề thi học viên giỏi, chúng ta và các em chăm chú theo dõi các nội dung bài viết khác trực thuộc chương trình toán lớp 5 trên hệ thống của Luyện Thi Nhanh nhé.
Mọi vướng mắc hoặc yêu cầu giải đáp bài bác toán, các bạn và các em có thể liên hệ qua điện thoại tư vấn hoặc zalo / facebook/ youtube. Luyện Thi Nhanh luôn mong ước ao hỗ trợ chúng ta và những em một cách xuất sắc nhất.






















Download tệp tin tổng hợp kiến thức toán lớp 5
3.7/5 - (325 bình chọn)
Trả lời Hủy
Bạn nên đăng nhập nhằm gửi phản bội hồi.
Thông báo bình luận qua email cho mình. Chúng ta cũng có thể theo dõi nhưng không đề nghị bình luận.
Có toàn bộ 64 bình Luận
← phản hồi trước
kien dep zai
Cho bản thân xin tệp tin với ạ!
Đăng nhập nhằm trả lời

Cho em xin với ạ
Đăng nhập nhằm trả lời

cho mình xin với
Đăng nhập nhằm trả lời

Gửi mail mang lại e với ạ, e thiết lập ko đc.
Đăng nhập để trả lời

Bài viết rất đầy đủ quá đi ạ.
Đăng nhập để trả lời

cho minh xin voi a vì tải về không dc a: duongvp.84
gmail.com
Đăng nhập nhằm trả lời

cho mình xin cùng với nhé
Đăng nhập để trả lời

Cô ơi mang lại e cài đặt BÀI NÀY VỀ VS AK
Đăng nhập nhằm trả lời

bài viết hữu ích. Mang lại e xin tệp tin với ạ. E cảm ơn các nhiều ạ!
Đăng nhập nhằm trả lời

cho e xin bạn dạng này với ạ
Đăng nhập nhằm trả lời
← Older Comments
Đáp án đề thi Toán vào lớp 6 Lương vậy Vinh 2021 – 2022
Đáp án đề thi giờ đồng hồ anh vào lớp 6 Amsterdam tp hà nội 2019
Đáp án đề thi toán vào lớp 6 Lương cầm cố Vinh 2020 – 2021
search quy khí cụ dãy số – điền số tiếp theo vào dãy số nâng cao
Đáp án đề thi trường đoản cú luận vào lớp 6 nai lưng Đại Nghĩa 2018 2019
Đáp án đề thi trắc nghiệm vào lớp 6 trằn Đại Nghĩa 2018 2019
Đáp án đề thi tự luận vào lớp 6 trằn Đại Nghĩa 2017 2018
Đáp án đề thi trắc nghiệm vào lớp 6 trần Đại Nghĩa 2017 – 2018
Đáp án đề thi trắc nghiệm vào lớp 6 trần Đại Nghĩa năm 2016 – 2017
Đáp án đề thi từ bỏ luận vào lớp 6 è cổ Đại Nghĩa 2016 2017
khảo sát tự luận vào lớp 6 nai lưng Đại Nghĩa 2015 – 2016
điều tra trắc nghiệm vào lớp 6 è Đại Nghĩa 2015 – 2016
Bài Viết Được xem Nhiều
Bài Giảng bắt đầu Nhất
13 bài bác toán chứng tỏ chia hết lớp 8 nâng cao
39 việc về giải phương trình lớp 8
Phương trình bậc cao lớp 8
Phương trình cất tham số Lớp 8
Giải phương trình chứa dấu giá trị tuyệt vời và hoàn hảo nhất lớp 8
Dạng toán Giải phương trình lớp 8 nâng cao – huyết 3
Đáp án đề thi Toán vào lớp 6 Lương núm Vinh 2021 – 2022
Tiết 2 Dạng Toán Giải Phương Trình Lớp 8 nâng cao
Lý thuyết các dạng toán phương trình ax+b=0 lớp 8 nâng cao
Tính cực hiếm biểu thức lớp 8 cải thiện – máu 1
Tìm x để biểu thức nguyên Lớp 8 (Tiết 1)
Rút gọn biểu thức toán lớp 8 nâng cấp (Ôn Tập – 2)
Chứng minh bất đẳng thức Lớp 8 – tiết 3
Phương pháp thông số bất định Lớp 8 nâng cao
Rút gọn gàng biểu thức toán lớp 8 nâng cấp (Ôn tập)
Tin Giáo Dục
Lái xuồng đưa học sinh đến trường mùa nước lũ
ngôi trường học hàng loạt lùi giờ học buổi sáng
trường tiểu học tập trả lại rộng 280 triệu vnd lạm thu
trường mầm non cấm đoán trẻ mang sữa, phân phối giá cấp đôi
Trẻ có tác dụng sai không chịu xin lỗi, bố mẹ nên có tác dụng gì?
<Đà Nẵng> Phẫn nộ gia sư tát, ném trẻ, cho ăn uống lại đồ nhả ra
Cậu nhỏ bé 11 tuổi bị bọn quét cuốn trôi cả 100m kể lại khoảng thời gian rất ngắn sinh tử
Lừa đảo đầu xuân năm mới học
4 lần biến đổi Sách Giáo Khoa
lý lẽ 7 khoản quỹ phụ huynh không được thu
Luyện Thi Nhanh
Chương trình đào tạo và giảng dạy của Luyện Thi Nhanh
Luyện thi nhanh được cách tân và phát triển từ năm 2009 tới thời điểm này với kim chỉ nam trở thành website chia sẻ về bài bác giảng và khuyên bảo luyện thi vào các trường chuyên quan trọng cho học viên từ lớp 5 đến lớp 10:Chương trình cơ bản theo cỗ GD&ĐTChương trình nâng cao - bộ GD&ĐTChương trình hocmai.vn
Tổng hợp những dạng toán nâng cao trong các đề thi
Hướng dẫn giải đề thi các năm của những trường chuyên
Hướng dẫn giải đề thi học viên giỏi
Đề thi rèn luyện theo công ty đề
Câu đố IQ cải cách và phát triển trí tuệ
Hỗ trợ lý giải giải trực tuyến
Chuyên Mục Nổi Bật
Bài Viết mới Nhất
Liên hệ Luyện Thi Nhanh
Follow
Luyen
Nhanh
Nhanh
Luyện Thi nhanh - Youtube chanel
Nội dung bản quyền thuộc Luyện Thi nhanh © 2018 - 2023














