Giải đáp học sinh - tìm môđun nhỏ dại nhất của một số trong những phức - thầy Đặng Thành Nam
Câu 34. Cho các số phức $z,w$ ưng ý $left| z^2-2z+5 ight|=left| (z-1+2i)(z+3i-1) ight|$ cùng $w=z-2+2i.$ Hỏi giá chỉ trị bé dại nhất của $left| w ight|$ là ?
A. $frac32.$
B. $1.$
C. $frac12.$
D. $2.$
Giải. Bạn đang xem: Tìm số phức có modun nhỏ nhất
Do đó $w=(1-2i)-2+2i=-1$ hoặc $w=z-2+2i=left( a-frac12i ight)-2+2i=left( a-2 ight)+frac32iRightarrow left| w ight|=sqrt(a-2)^2+frac94ge frac32.$ đối chiếu hai trường hợp, ta có $left| w ight|ge 1.$ Chọn câu trả lời B.

Vted thông tin chương trình Ưu đãi học phí những khoá học tập Vted giành riêng cho K99 từ thời điểm ngày 2 tháng 04 năm 2017 cho hết ngày thứ 8 tháng 04 năm 2017 như sau:

| STT | KHOÁ HỌC | HỌC PHÍ GỐC | HỌC PHÍ ƯU ĐÃI | LINK ĐĂNG KÍ |
| 1 | LUYỆN ĐỀ TOÁN (30 ĐỀ) | 400.000Đ | 200.000Đ | ĐĂNG KÍ |
| 2 | TƯ DUY TRẮC NGHIỆM TOÁN | 400.000Đ | 200.000Đ | ĐĂNG KÍ |
| 3 | BÁM SÁT TOÀN DIỆN TOÁN 12 | 800.000Đ | 400.000Đ | ĐĂNG KÍ |
| 4 | NHÓM CÂU HỎI VẬN DỤNG THỰC TIỄN | 200.000Đ | 100.000Đ | ĐĂNG KÍ |
*Chú ý: các em muốn tăng thêm điểm số đạt 9-10 bắt buộc đăng kí đôi khi khoá tứ duy trắc nghiệm và Luyện đề:
Riêng các em học sinh 2000 trở đi rất có thể tham khảo khoá học: PRO X TOÁN 2018 tại Vted được xây dựng giành riêng cho các em trên đây:http://vted.vn/khoa-hoc/xem/pro-x-luyen-thi-thpt-quoc-gia-mon-toan-2018-kh522847554.html
(Video reviews khoá PRO X TOÁN 2018 tại Vted)
(Video trình làng lộ trình Khoá PRO X TOÁN 2018 trên Vted)
Các em là học viên 2000 bây giờ là lớp 11 sẵn sàng lên lớp 12 theo dõi đến thầy khoá PRO X TOÁN 2018 tại Vted sau đây:
Bài viết hướng dẫn cách thức giải việc tìm giá chỉ trị lớn nhất và giá chỉ trị nhỏ dại nhất của môđun số phức vừa lòng điều kiện cho trước (cách hotline khác: GTLN – GTNN môđun số phức, Min – Max môđun số phức) trong công tác Giải tích 12, đây là dạng toán áp dụng cao (nâng cao, khó) thường gặp gỡ trong các đề thi trắc nghiệm Toán 12 với đề thi THPT quốc gia môn Toán.
I. PHƯƠNG PHÁP GIẢI TOÁN1. Phương pháp chung+ tìm tập hòa hợp điểm biểu diễn các số phức $z$ thỏa đk cho trước.+ Vẽ tập hợp điểm màn biểu diễn lên hệ trục, từ kia suy ra kết quả.
2. Một số hiệu quả thường dùnga) câu hỏi 1: Trong khía cạnh phẳng, mang lại điểm $O$ và mặt đường tròn $C(I;R)$ nắm định, $M$ là điểm di động trê tuyến phố tròn đó. Tra cứu $OM_min $, $OM_max .$+ ví như $O$ nằm đi ngoài đường tròn thì:$OM_min = OA = OI – R.$$OM_max = OB = OI + R.$
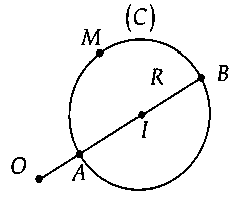
+ giả dụ $O$ nằm trên phố tròn thì:$OM_min = 0.$$OM_max = OB = 2R.$
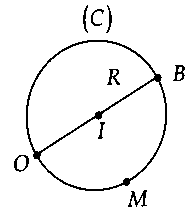
+ giả dụ $O$ bên trong đường tròn thì:$OM_min = OA = R – OI.$$OM_max = OB = OI + R.$
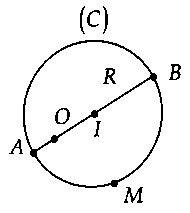
b) vấn đề 2: Trong khía cạnh phẳng, đến điểm $O$ và con đường thẳng $d$ nỗ lực định, $M$ là vấn đề di động trên đường thẳng đó. Search $OM_min .$+ ví như $O$ nằm ngoài đường thẳng $d$ thì: $OM_min = OH = d(O;d).$
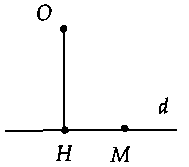
+ ví như $O$ nằm trên đường tròn thì $OM_min = 0.$
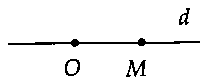
c) câu hỏi 3: Trong mặt phẳng, cho hai tuyến đường thẳng riêng biệt $d$, $d’$ cố kỉnh định; $M$ là điểm di động trên phố thẳng $d$ với $N$ là vấn đề di động trên phố thẳng $d’.$ tìm kiếm $MN_min .$+ nếu như $d//d’$ thì $MN_min = OH = dleft( d;d’ ight).$
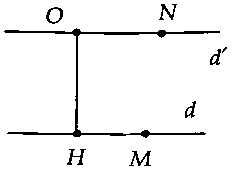
+ nếu $d$ với $d’$ giảm nhau thì $MN_min = 0.$
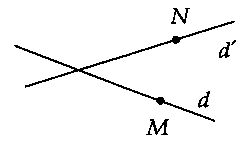
d) câu hỏi 4: Trong khía cạnh phẳng, cho hai tuyến đường thẳng $d$ và mặt đường tròn $C(I;R)$ cố định và thắt chặt và không tồn tại điểm bình thường với nhau; $M$ là điểm di động trên đường thẳng $d$ với $N$ là điểm di động trên phố tròn $C(I;R).$ tra cứu $MN_min .$
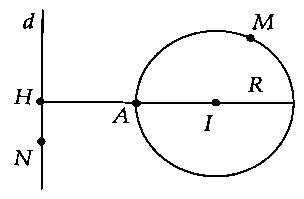
$MN_min = AH = d(I;d) – R.$
e) bài toán 5: Trong khía cạnh phẳng, cho tía điểm $O$, $A$, $B$ thắt chặt và cố định không trực tiếp hàng; $M$ là điểm di cồn trên đoạn trực tiếp $AB.$ tìm $OM_min $, $OM_max .$+ nếu $widehat AOB$ là góc nhọn thì:$OM_min = min OA;OB .$$OM_max = max OA;OB .$
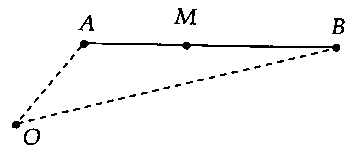
+ trường hợp $widehat AOB$ là góc tù đọng thì:$OM_min = d(O;AB).$$OM_max = max OA;OB .$
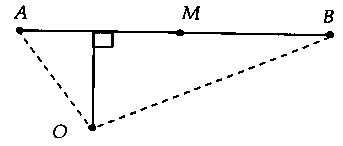
II. BÀI TẬP TRẮC NGHIỆM MINH HỌAVí dụ 1: đến số phức $z$ vừa lòng điều kiện $|z – 1 – 2i| = 2.$ call $M$, $m$ lần lượt là giá bán trị lớn nhất và giá trị nhỏ tuổi nhất của $|z|.$ cực hiếm $M + m$ bằng?
A. $2sqrt 5 .$B. $sqrt 5 .$C. $sqrt 5 + 2.$D. $sqrt 5 – 2.$
Lời giải:Gọi $P(x;y)$ là vấn đề biểu diễn của số phức $z = x + yi$ $(x;y in R)$ trên khía cạnh phẳng tọa độ.
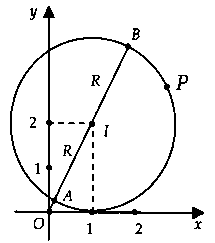
Ta có: $|z – 1 – 2i| = 2$ $ Leftrightarrow (x – 1)^2 + (y – 2)^2 = 4.$Suy ra tập hợp điểm biểu diễn những số phức $z$ là đường tròn $(C)$ có tâm $I(1;2)$ và nửa đường kính $R = 2.$Từ hình vẽ, ta có:$M = |z_max = OB = OI + R$ với $m = |z = OA = OI – R.$Vậy $M + m = 2OI$ $ = 2sqrt 1^2 + 2^2 = 2sqrt 5 .$Chọn lời giải A.Chú ý: trường hợp $(C)$ qua gốc tọa độ $O$ thì $m =0$, $M = 2R.$
Ví dụ 2: cho số phức $z$ thỏa mãn điều kiện $|z – 2 + i| = 1.$ call $M$, $m$ theo thứ tự là giá bán trị lớn số 1 và giá bán trị nhỏ nhất của $|z|.$ quý giá $M+3m$ bằng:A. $4sqrt 5 – 4.$B. $4sqrt 5 – 2.$C. $2sqrt 5 + 2.$D. $2sqrt 5 – 2.$
Lời giải:Gọi $P(x;y)$ là điểm biểu diễn của số phức $z = x + yi$ $(x;y in R)$ trên mặt phẳng tọa độ.Ta có: $|z – 2 + i| = 1$ $ Leftrightarrow (x – 2)^2 + (y + 1)^2 = 1.$Suy ra tập đúng theo điểm biểu diễn các số phức $z$ là con đường tròn $(C)$ tất cả tâm $I(2;-1)$ và bán kính $R=1.$
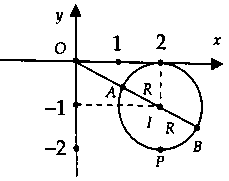
Từ hình vẽ, ta có:$M = |z = OB = OI + R$ và $m = |z_min = OA = OI – R.$Vậy $M + 3m = 4OI – 2R = 4sqrt 5 – 2.$Chọn lời giải B.
Ví dụ 3: đến số phức $z$ vừa lòng điều khiếu nại $|z + i| = sqrt 2 |z – 1|.$ hotline $M$, $m$ theo lần lượt là giá trị lớn số 1 và giá chỉ trị nhỏ nhất của $|z|.$ giá trị $M^2 – m^2$ bằng?
A. $9.$B. $8sqrt 5 .$C. $4sqrt 5 .$D. $2sqrt 5 .$
Lời giải:Gọi $P(x;y)$ là vấn đề biểu diễn của số phức $z = x + yi$ $(x;y in R)$ trên mặt phẳng tọa độ.Ta có: $|z + i| = sqrt 2 |z – 1|.$$ Leftrightarrow sqrt x^2 + (y + 1)^2 $ $ = sqrt 2 sqrt (x – 1)^2 + y^2 .$$ Leftrightarrow x^2 + y^2 + 2y + 1$ $ = 2left( x^2 – 2x + 1 + y^2 ight).$$ Leftrightarrow x^2 + y^2 – 4x – 2y + 1 = 0.$Suy ra tập thích hợp điểm biểu diễn những số phức $z$ là con đường tròn $(C)$ có tâm $I(2;1)$ và nửa đường kính $R = 2.$
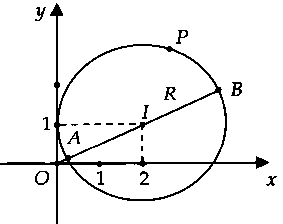
Từ hình vẽ, ta có: $M = |z_max = OB = OI + R$ với $m = |z_min = OA = OI – R.$Vậy $M^2 – m^2$ $ = (OI + R)^2 – (OI – R)^2$ $ = 4OI.R = 8sqrt 5 .$Chọn giải đáp B.
Ví dụ 4: đến số phức $z$ thỏa mãn nhu cầu điều kiện $|z + i| = 3.$ hotline $M$, $m$ thứu tự là giá bán trị lớn nhất và giá bán trị nhỏ tuổi nhất của $|z – 1 – 2i|.$ cực hiếm $M + 2m$ bằng?
A. $27.$B. $21.$C. $3sqrt 10 – 3.$D. $3sqrt 10 – 9.$
Lời giải:Gọi $P(x;y)$ là điểm biểu diễn của số phức $z = x + yi$ $(x;y in R)$ trên phương diện phẳng tọa độ.Ta có: $|z + i| = 3$ $ Leftrightarrow x^2 + (y + 1)^2 = 9.$$ Leftrightarrow <(x – 1) + 1>^2 + <(y – 2) + 3>^2 = 9.$Ta có số phức $z – 1 – 2i$ gồm điểm trình diễn là $P"(x – 1;y – 2).$ Suy ra tập đúng theo điểm biểu diễn những số phức $z – 1 – 2i$ là mặt đường tròn $(C)$ có tâm $I( – 1; – 3)$ và bán kính $R=3.$
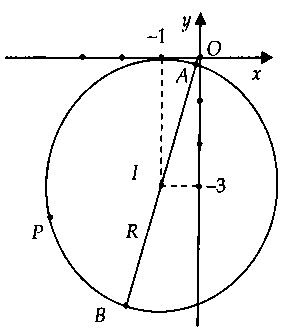
Từ hình vẽ, ta có:$M = |z – 1 – 2i_max $ $ = OB = OI + R$ và $m = |z – 1 – 2i$ $ = OA = OI – R.$Vậy $M + 2m = 3OI – R = 3sqrt 10 – 3.$Chọn giải đáp C.
Ví dụ 5: mang lại số phức $z$ thỏa mãn điều khiếu nại $|z – 2 – i| = |z + 1|.$ điện thoại tư vấn $m$ là giá trị giá trị nhỏ tuổi nhất của $|z|.$ Giá trị $m$ bằng?
A. $2.$B. $fracsqrt 10 5.$C. $frac23.$D. $frac15.$
Lời giải:Gọi $M(x;y)$ là điểm biểu diễn của số phức $z = x + yi$ $(x;y in R)$ cùng bề mặt phẳng tọa độ.Ta có: $|z – 2 – i| = |z + 1|.$$ Leftrightarrow sqrt (x – 2)^2 + (y – 1)^2 $ $ = sqrt (x + 1)^2 + y^2 .$$ Leftrightarrow x^2 – 4x + 4 + y^2 – 2y + 1$ $ = x^2 + 2x + 1 + y^2.$$ Leftrightarrow 3x + y – 2 = 0.$Suy ra tập hòa hợp điểm biểu diễn các số phức $z$ là con đường thẳng $d:$ $3x + y – 2 = 0.$
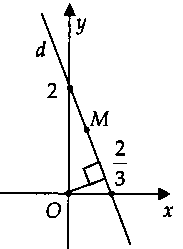
Từ hình vẽ, ta có:$m = |z_min = d(O;d)$ $ = fracsqrt 3^2 + 1^2 = fracsqrt 10 5.$Chọn đáp án B.Chú ý: giả dụ $d$ qua cội tọa độ $O$ thì $m =0.$
Ví dụ 6: trong số số phức thỏa mãn điều kiện $|z – 1 – i| = |z – 2i|.$ tìm kiếm số phức $z$ tất cả môđun nhỏ nhất.A. $z = frac12 – frac12i.$B. $z = frac12 + frac32i.$C. $z = – frac12 + frac12i.$D. $z = frac32 – frac12i.$
Lời giải:Đặt $z = x + yi$ $(x,y in R).$Ta có $|z – 1 – i| = |z – 2i|$ $ Leftrightarrow (x – 1)^2 + (y – 1)^2$ $ = x^2 + (y – 2)^2$ $ Leftrightarrow y = x + 1.$$|z| = sqrt x^2 + y^2 $ $ = sqrt 2x^2 + 2x + 1 $ $ = sqrt 2left( x + frac12 ight)^2 + frac12 ge fracsqrt 2 2.$Do kia $|z|$ nhỏ nhất khi còn chỉ khi $x = – frac12$, $y = frac12$ $ Rightarrow z = – frac12 + frac12i.$Chọn đáp án C.
Ví dụ 7: đến số phức $z_1$ thỏa mãn điều kiện $left| z_1 – 1 – i
ight| = left| z_1 – 2
ight|$, số phức $z_2$ thỏa mãn điều kiện $left| z_2 – 1
ight| = left| z_2 – i
ight|.$ hotline $m$ là cực hiếm giá trị nhỏ nhất của $left| z_2 – z_1
ight|.$ quý hiếm $m$ bằng?
A. $2.$B. $frac12.$C. $fracsqrt 2 2.$D. $fracsqrt 3 3.$
Lời giải:Gọi $P_1left( x_1;y_1 ight)$ là vấn đề biểu diễn của số phức $z_1 = x_1 + y_1i$ $left( x_1;y_1 in R ight)$ trên khía cạnh phẳng tọa độ.Ta có: $left| z_1 – 1 – i ight| = left| z_1 – 2 ight|$ $ Leftrightarrow sqrt left( x_1 – 1 ight)^2 + left( y_1 – 1 ight)^2 $ $ = sqrt left( x_1 – 2 ight)^2 + y_1^2 .$$ Leftrightarrow x_1^2 – 2x_1 + 1 + y_1^2 – 2y_1 + 1$ $ = x_1^2 – 4x_1 + 4 + y_1^2.$$ Leftrightarrow x_1 – y_1 – 1 = 0.$Suy ra tập hòa hợp điểm biểu diễn các số phức $z_1$ là con đường thẳng $d_1:x – y – 1 = 0.$Gọi $P_2left( x_2;y_2 ight)$ là điểm biểu diễn của số phức $z_2 = x_2 + y_2i$ $left( x_2;y_2 in R ight)$ trên phương diện phẳng tọa độ.Ta có: $left| z_2 – 1 ight| = left| z_2 – i ight|.$$ Leftrightarrow sqrt left( x_2 – 1 ight)^2 + y_2^2 = sqrt x_2^2 + left( y_2 – 1 ight)^2 $ $ Leftrightarrow x_2 – y_2 = 0.$Suy ra tập thích hợp điểm biểu diễn các số phức $z_2$ là mặt đường thẳng: $d_2:x – y = 0.$Ta có: $left| z_2 – z_1 ight|$ $ = sqrt left( x_2 – x_1 ight)^2 + left( y_2 – y_1 ight)^2 $ $ = P_1P_2$ $ Rightarrow z_2 – z_1 ight = dleft( d_1;d_2 ight).$Vì $O in d_2$ $ Rightarrow z_2 – z_1 ight = dleft( d_1;d_2 ight)$ $ = dleft( O;d_1 ight) = fracsqrt 2 2.$Chọn giải đáp C.
Ví dụ 8: mang lại số phức $z_1$ thỏa mãn $left| z_1 – 1 – 2i ight| = 2$ cùng số phức $z_2$ thỏa mãn $left| z_2 – 1 ight| = left| z_2 + i ight|.$ Tính giá trị nhỏ tuổi nhất của $left| z_1 – z_2 ight|.$A. $frac2sqrt 2 – 22.$B. $frac3sqrt 2 – 42.$C. $frac3sqrt 2 – 44.$D. $frac3sqrt 2 – 24.$
Lời giải:Gọi $P$, $Q$ lần lượt là điểm biểu diễn số phức $z_1$, $z_2$ trên khía cạnh phẳng tọa độ.
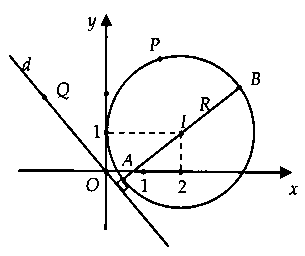
$left| z_1 – 1 – 2i ight| = 2$ $ Rightarrow p in (C)$ bao gồm tâm $I(1;2)$, bán kính $R =2.$Gọi $z_2 = x_2 + y_2i$ $left( x_2;y_2 in R ight).$$left| z_2 – 1 ight| = left| z_2 + i ight|$ $ Leftrightarrow x_2 + y_2 = 0.$$ Rightarrow Q in d:x + y = 0.$Ta có: $left| z_1 – z_2 ight| = PQ$ $ Rightarrow _min = PQ_min $, $d(I;d) = frac3sqrt 2 2.$Từ mẫu vẽ ta có: $PQ_min = d(I;d) – R$ $ = frac3sqrt 2 2 – 2$ $ = frac3sqrt 2 – 42.$Chọn giải đáp B.
Ví dụ 9: cho số phức $z_1$ thỏa mãn nhu cầu $left| z_1 – 2 + i ight| = 1$ và số phức $z_2$ thỏa mãn nhu cầu $left| z_2 + 2i ight| = left| z_2 + 2 ight|.$ Tính giá chỉ trị nhỏ tuổi nhất của $left| z_1 – z_2 ight|.$A. $frac3sqrt 2 – 22.$B. $frac3sqrt 2 – 24.$C. $frac3sqrt 2 – 14.$D. $frac3sqrt 2 – 12.$
Lời giải: call $M$, $N$ lần lượt là vấn đề biểu diễn số phức $z_1$, $z_2$ trên mặt phẳng tọa độ.
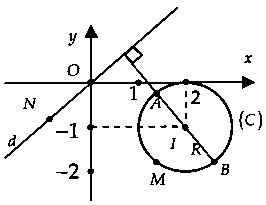
$left| z_1 – 2 + i ight| = 1$ $ Rightarrow M in (C)$ gồm tâm $I(2; – 1)$, nửa đường kính $R=1.$Gọi $z_2 = x_2 + y_2i$ $left( x_2;y_2 in R ight).$$left| z_2 + 2i ight| = left| z_2 + 2 ight|$ $ Leftrightarrow x_2 – y_2 = 0.$$ Rightarrow N in d:x – y = 0.$Ta có: $left| z_1 – z_2 ight| = MN$ $ Rightarrow z_1 – z_2 ight = MN_min $, $d(I;d) = frac3sqrt 2 2.$Từ hình mẫu vẽ ta có: $MN_min = d(I;d) – R$ $ = frac3sqrt 2 2 – 1$ $ = frac3sqrt 2 – 22.$Chọn câu trả lời A.
Ví dụ 10: mang đến số phức $z_1$ thỏa mãn nhu cầu $left| z_1 – 2 – 3i
ight| = 2$ và số phức $z_2$ thỏa mãn $left| z_2 + 1 + 2i
ight| = left| z_2 + i
ight|.$ điện thoại tư vấn $M$ là giá bán trị lớn nhất của $left| z_1
ight|$, $m$ là giá bán trị nhỏ tuổi nhất của $left| z_2
ight|.$ quý hiếm $M – m^2$ bằng?
A. $sqrt 13 + sqrt 2 – 2.$B. $sqrt 13 – 4.$C. $sqrt 13 .$D. $sqrt 13 – sqrt 2 – 2.$
Lời giải:Gọi $P$, $Q$ lần lượt là điểm biểu diễn số phức $z_1$, $z_2$ trên phương diện phẳng.
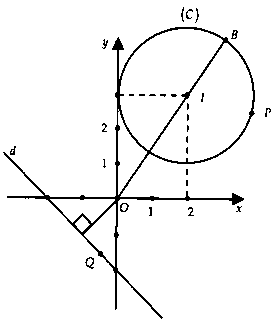
$left| z_1 – 2 – 3i ight| = 2$ $ Rightarrow phường in (C)$ bao gồm tâm $I(2;3)$, bán kính $R =2.$Gọi $z_2 = x_2 + y_2i$ $left( x_2;y_2 in R ight).$$left| z_2 + 1 + 2i ight| = left| z_2 + i ight|$ $ Leftrightarrow x_2 + y_2 + 2 = 0.$$ Rightarrow Q in d:x + y + 2 = 0.$Từ hình vẽ ta có:$M = left$ $ = OB = OI + R$ $ = sqrt 13 + 2$, $m = z_2 ight$ $ = d(O;d) = sqrt 2 .$$ Rightarrow M – m^2 = sqrt 13 .$Chọn lời giải C.
Ví dụ 11: cho số phức $z_1$ vừa lòng $left| z_1 – 3 – 5i ight| = 2$ cùng số phức $z_2$ vừa lòng $left| z_2 + 1 + 2i ight| = left| z_2 + i ight|.$ Tính giá chỉ trị nhỏ nhất của $left| z_1 – z_2 – 1 – 2i ight|.$A. $frac5sqrt 2 – 42.$B. $frac5sqrt 2 + 42.$C. $frac7sqrt 2 – 42.$D. $frac7sqrt 2 + 42.$
Lời giải:Ta có: $left| z_1 – z_2 – 1 – 2i ight|$ $ = left| left( z_1 – 1 – 2i ight) – z_2 ight|$ $ = left| z_3 – z_2 ight|$ cùng với $z_3 = z_1 – 1 – 2i.$
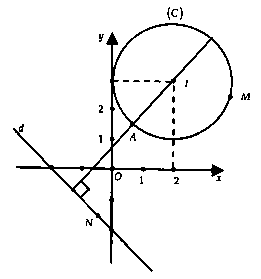
Gọi $M$, $N$ lần lượt là điểm biểu diễn số phức $z_3$, $z_2$ trên khía cạnh phẳng tọa độ.$left| z_1 – 3 – 5i ight| = 2$ $ Leftrightarrow left| underbrace z_1 – 1 – 2i_z_3 – 2 – 3i ight| = 2.$$ Rightarrow M in (C)$ có tâm $I(2;3)$, nửa đường kính $R = 2.$Gọi $z_2 = x + yi$ $(x;y in R)$, $left| z_2 + 1 + 2i ight| = left| z_2 + i ight|.$$ Leftrightarrow x + y + 2 = 0$ $ Rightarrow N in d:x + y + 2 = 0.$Ta có: $d(I;d) = frac7sqrt 2 2.$Từ hình mẫu vẽ ta tất cả $MN_min = d(A;d)$ $ = d(I;d) – R$ $ = frac7sqrt 2 2 – 2$ $ = frac7sqrt 2 – 42.$Chọn lời giải C.
Ví dụ 12: cho số phức $z$ vừa lòng điều kiện $|z – 1 – i| + |z – 2 – 3i| = sqrt 5 .$ gọi $M$, $m$ thứu tự là giá trị lớn số 1 và giá trị nhỏ tuổi nhất của môđun của $z.$ quý hiếm $M^2 + m^2$ bằng?
A. $11.$B. $15.$C. $sqrt 2 + sqrt 13 .$D. $frac665.$
Lời giải:Gọi $P(x;y)$ là vấn đề biểu diễn của số phức $z = x + yi$ $(x;y in R)$ trên mặt phẳng tọa độ.
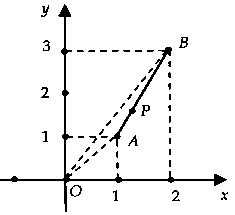
Ta có: $|z – 1 – i| + |z – 2 – 3i| = sqrt 5 .$$ Leftrightarrow sqrt (x – 1)^2 + (y – 1)^2 $ $ + sqrt (x – 2)^2 + (y – 3)^2 $ $ = sqrt 5 $ $(1).$Đặt $A(1;1)$, $B(2;3)$ thì trường đoản cú $(1)$ ta có: $AP + BP = sqrt 5 $ $(2).$Mặt không giống $AB = sqrt (2 – 1)^2 + (3 – 1)^2 = sqrt 5 $ $(3).$Từ $(2)$ và $(3)$ suy ra $P$ thuộc đoạn thẳng $AB.$Từ mẫu vẽ ta có:$M = |z_max = OB = sqrt 13 $ với $m = |z = OA = sqrt 2 $ $ Rightarrow M^2 + m^2 = 15.$Chọn đáp án B.
Ví dụ 13: đến số phức $z$ thỏa mãn nhu cầu điều khiếu nại $|z – 2i| + |z – 4 – 3i| = sqrt 17 .$ call $M$, $m$ lần lượt là giá chỉ trị lớn nhất và giá bán trị nhỏ dại nhất của $|z|.$ Giá trị $M + m$ bằng?
A. $sqrt 5 + sqrt 2 .$B. $frac8sqrt 17 7 + 5.$C. $frac8sqrt 17 7 + 2.$D. $7.$
Lời giải:Gọi $P(x;y)$ là điểm biểu diễn của số phức $z = x + yi$ $(x;y in R)$ trên phương diện phẳng tọa độ.
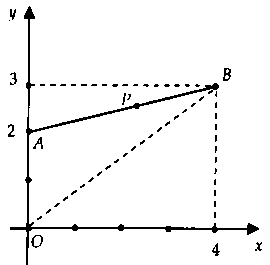
Ta có: $|z – 2i| + |z – 4 – 3i| = sqrt 17 .$$ Leftrightarrow sqrt x^2 + (y – 2)^2 $ $ + sqrt (x – 4)^2 + (y – 3)^2 $ $ = sqrt 17 $ $(1).$Đặt $A(0;2)$, $B(4;3)$ thì từ $(1)$ ta có: $AP + BP = sqrt 17 $ $(2).$Mặt không giống $AB = sqrt (4 – 0)^2 + (3 – 2)^2 = sqrt 17 $ $(3).$Từ $(2)$ với $(3)$ suy ra $P$ trực thuộc đoạn trực tiếp $AB.$Từ hình vẽ ta có: $M = |z_max = OB = 5$ cùng $m = |z_min = OA = 2$ $ Rightarrow M + m = 7.$Chọn đáp án D.
Ví dụ 14: Xét các số phức $z$ thỏa mãn $|z + 2 – i| + |z – 4 – 7i| = 6sqrt 2 .$ điện thoại tư vấn $m$, $M$ lần lượt là giá chỉ trị bé dại nhất cùng giá trị lớn nhất của $|z|.$ quý giá $m + M$ bằng?
A. $frac2sqrt 65 + 3sqrt 2 2.$B. $frac2sqrt 65 + sqrt 2 2.$C. $frac2sqrt 65 + sqrt 2 4.$D. $frac2sqrt 65 + 3sqrt 2 2.$
Lời giải:Gọi $P(x;y)$ là vấn đề biểu diễn của số phức $z = x + yi$ $(x;y in R)$ trên mặt phẳng tọa độ.
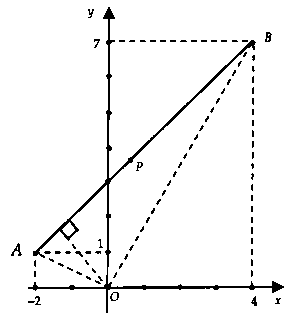
Ta có: $|z + 2 – i| + |z – 4 – 7i| = 6sqrt 2 .$$ Leftrightarrow sqrt (x + 2)^2 + (y – 1)^2 $ $ + sqrt (x – 4)^2 + (y – 7)^2 = 6sqrt 2 .$Đặt $A( – 2;1)$, $B(4;7)$ thì tự $(1)$ ta có: $AP + BP = 6sqrt 2 $ $(2).$Mặt không giống $AB = 6sqrt 2 $ $(3).$Từ $(2)$ với $(3)$ suy ra $P$ trực thuộc đoạn thẳng $AB.$Từ mẫu vẽ ta có: $M = |z = OB = sqrt 65 .$$AB:fracx + 24 + 2 = fracy – 17 – 1$ $ Leftrightarrow x – y + 3 = 0$, $m = |z_min $ $ = d(O;AB) = frac3sqrt 2 2.$$ Rightarrow M + m = sqrt 65 + frac3sqrt 2 2$ $ = frac2sqrt 65 + 3sqrt 2 2.$Chọn câu trả lời A.
Ví dụ 15: Xét những số phức $z$ vừa lòng $|z + 2 – i| + |z – 4 – 7i| = 6sqrt 2 .$ call $m$, $M$ theo thứ tự là giá bán trị nhỏ nhất cùng giá trị lớn nhất của $|z – 1 + i|.$ Tính $P = m + M.$A. $P = sqrt 13 + sqrt 73 .$B. $P = frac5sqrt 2 + 2sqrt 73 2.$C. $P = 5sqrt 2 + sqrt 73 .$D. $P = frac5sqrt 2 + sqrt 73 2.$
Lời giải:Gọi $P(x;y)$ là điểm biểu diễn của số phức $z = x + yi$ $(x;y in R)$ xung quanh phẳng tọa độ.Số phức $z-1+i$ có điểm trình diễn là $P"(x – 1;y + 1).$Ta có: $|z + 2 – i| + |z – 4 – 7i| = 6sqrt 2 .$$ Leftrightarrow sqrt (x + 2)^2 + (y – 1)^2 $ $ + sqrt (x – 4)^2 + (y – 7)^2 $ $ = 6sqrt 2 .$$ Leftrightarrow sqrt ((x – 1) + 3)^2 + ((y + 1) – 2)^2 $ $ + sqrt ((x – 1) – 3)^2 + ((y + 1) – 8)^2 $ $ = 6sqrt 2 $ $(1).$Đặt $A(-3;2)$, $B(3;8)$ thì trường đoản cú $(1)$ ta có: $AP’ + BP’ = 6sqrt 2 $ $(2).$Mặt khác $AB = 6sqrt 2 $ $(3).$Từ $(2)$ với $(3)$ suy ra $P’$ ở trong đoạn trực tiếp $AB.$
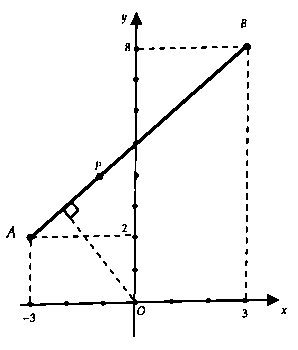
Từ hình vẽ ta có: $M = |z_max = OB = sqrt 73 .$$AB:$ $fracx + 33 + 3 = fracy – 28 – 2$ $ Leftrightarrow x – y + 5 = 0.$$m = |z_min $ $ = d(O;AB) = frac5sqrt 2 2.$$ Rightarrow M + m$ $ = sqrt 73 + frac5sqrt 2 2$ $ = frac2sqrt 73 + 5sqrt 2 2.$Chọn đáp án B.
III. LUYỆN TẬP1. ĐỀ BÀICâu 1: mang đến số phức $z$ thỏa mãn nhu cầu điều kiện $|z + 1 – 3i| = 2.$ hotline $M$, $m$ thứu tự là giá bán trị lớn số 1 và giá chỉ trị bé dại nhất của $|z|.$ Giá trị $M.m$ bằng?
A. $14.$B. $1.$C. $8.$D. $6.$
Câu 2: cho số phức $z$ thỏa mãn nhu cầu điều khiếu nại $|z + 1 + i| = 3.$ call $M$, $m$ theo thứ tự là giá trị lớn nhất và giá chỉ trị nhỏ nhất của $|z|.$ Giá trị $M – m$ bằng?
A. $12.$B. $6.$C. $2sqrt 2 .$D. $3 + sqrt 2 .$
Câu 3: đến số phức $z$ thỏa mãn điều kiện $|z – 2| = 2.$ điện thoại tư vấn $M$, $m$ theo thứ tự là giá trị lớn nhất và giá trị nhỏ tuổi nhất của $|z + i|.$ giá trị $M – 2m$ bằng?
A. $1.$B. $3sqrt 5 – 2.$C. $3sqrt 5 – 6.$D. $6 – sqrt 5 .$
Câu 4: đến số phức $z$ thỏa mãn điều khiếu nại $|z – 1| = |z + 1 – i|.$ call $m$ là giá chỉ trị bé dại nhất của $|z|.$ Giá trị $m$ bằng?
A. $frac120.$B. $fracsqrt 5 10.$C. $frac14.$D. $frac12.$
Câu 5: cho số phức $z_1$ thỏa mãn nhu cầu điều kiện $left| z_1 + 1 – i
ight| = left| z_1 + 2
ight|$, số phức $z_2$ thỏa mãn điều khiếu nại $left| z_2 – 1
ight| = left| z_2 + i
ight|.$ call $m$ là giá bán trị nhỏ tuổi nhất của $left| z_2 – z_1
ight|.$ Giá trị $m$ bằng?
A. $2.$B. $frac12.$C. $fracsqrt 2 2.$D. $fracsqrt 3 3.$
Câu 6: mang đến số phức $z_1$ thỏa mãn nhu cầu $left| z_1 – 2 – 3i ight| = 1$ cùng số phức $z_2$ thỏa mãn nhu cầu $left| z_2 + i ight| = left| z_2 – 1 ight|.$ Tính giá trị nhỏ nhất của $left| z_1 – z_2 ight|.$A. $frac3sqrt 2 – 22.$B. $frac3sqrt 2 – 24.$C. $frac3sqrt 2 – 44.$D. $frac3sqrt 2 – 42.$
Câu 7: đến số phức $z_1$ vừa lòng $left| (1 + i)z_1 + 1 – 5i
ight| = 2sqrt 2 $ cùng số phức $z_2$ vừa lòng $left| z_2 + 1 + 2i
ight| = left| z_2 + i
ight|.$ gọi $m_1$ là giá bán trị nhỏ nhất của $left| z_1
ight|$, $m_2$ là giá chỉ trị bé dại nhất của $left| z_2
ight|.$ quý giá $m_1 + m_2$ bằng?
A. $sqrt 13 – 4.$B. $sqrt 13 – 2sqrt 2 .$C. $sqrt 13 – 2 + sqrt 2 .$D. $sqrt 13 + 2sqrt 2 .$
Câu 8: mang đến số phức $z_1$ vừa lòng $left| z_1 + 1 – 3i
ight| = 2$ với số phức $z_2$ vừa lòng $left| z_2 – 1 + i
ight| = left| z_2 – i
ight|.$ hotline $M$, $m$ là giá chỉ trị lớn nhất của $left| z_1
ight|$ và giá trị nhỏ tuổi nhất của $left| z_2
ight|.$ Giá trị $M.m$ bằng?
A. $frac2sqrt 5 + 5sqrt 2 10.$B. $frac5sqrt 2 – 2sqrt 5 10.$C. $frac10 + sqrt 10 10.$D. $frac5sqrt 2 – 2sqrt 5 5.$
Câu 9: đến số phức $z$ thỏa mãn nhu cầu điều khiếu nại $|z + 2 – i| + |z – 2 – 3i| = 2sqrt 5 .$ gọi $M$, $m$ theo thứ tự là giá bán trị lớn nhất và giá trị bé dại nhất của môđun của $z$, tính $M+m.$A. $frac4sqrt 5 + 5sqrt 13 5.$B. $sqrt 5 + sqrt 13 .$C. $sqrt 2 + sqrt 13 .$D. $sqrt 2 + 2sqrt 13 .$
Câu 10: đến số phức $z$ thỏa mãn nhu cầu điều khiếu nại $|z + 2 – i| + |z – 2 – 3i| = 2sqrt 5 .$ hotline $M$, $m$ lần lượt là giá bán trị lớn nhất và giá chỉ trị nhỏ tuổi nhất của môđun của $z + 1 – 2i$, tính $M+m.$A. $frac2sqrt 5 + 5sqrt 10 5.$B. $fracsqrt 5 + 5sqrt 10 5.$C. $sqrt 2 + sqrt 10 .$D. $sqrt 2 + 2sqrt 10 .$














