Cách Tính Delta, Delta Phẩy: Công Thức Đen Ta Phẩy Phương Trình Bậc 2

Ví dụ: đến phương trình x2 + 4x – 2 = 0 . Search nghiệm của phương trình bậc 2 trên

Trước không còn tính detla Δ = b2 – 4ac = 4*4 – 4*2*1 = 8 .

Vì Δ = 8 > 0 cần phương trình sẽ sở hữu được 2 nghiệm minh bạch là:

CÔNG THỨC TÍNH DELTA PHẨY:

Δ’ = b’2 – ac

Công thức này được hotline là công thức nghiệm thu sát hoạch gọn

Ví dụ: đến phương trình x² – 2(m+1)x + m² + m +1 = 0

a . Tìm các giá trị của m nhằm phương trình tất cả nghiệm

b . Trong trường thích hợp phương trình gồm nghiệm là x1, x2 hãy tính theo m :

x1+ x2 ; x1* x2 ; (x1)² +( x2)²

Đáp số:

a . Δ′ = m + 2 >= 0 lúc m >= -2

b . x1 + x2 = 2(m +1)

x1 * x2 = m² + m – 1

(x1)² + (x2)² = (x1 + x2)² – 2 (x1* x2)

= 4m² + 8m +4 – 2m² – 2m + 2

= 2m² + 6m +6

Hệ thức Viet

Nếu ta gồm x1, x2 là nghiệm của phương trình: ax2 + bx +c = 0

thì: x1; x2: S = x1 + x2 = -b/a

P = x1 . X2 = c/a

II . Bài tập vận dụng công thức tính đelta cùng đental phẩy phương trình bậc 2

Bài 1: cho phương trình

a) minh chứng rằng phương trình luôn có nghiệm với đa số k.

b) tìm k nhằm phương trình bao gồm hai nghiệm cùng dấu. Lúc ấy hai nghiệm mang dấu gì?

c) tìm k nhằm phương trình bao gồm tổng nhì nghiệm bởi 6. Tìm hai nghiệm đó.

Giải:

a) Phương trình đã cho rằng phương trình bậc hai.

Bài 2. Cho phương trình:

Bài 3: Gọi m cùng n là những nghiệm của phương trình

Hiển nhiên m, n những khác -1 với -1 không thoản mãn phương trình (1).

Ta có:

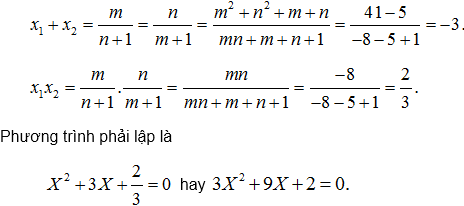
Bài 4:

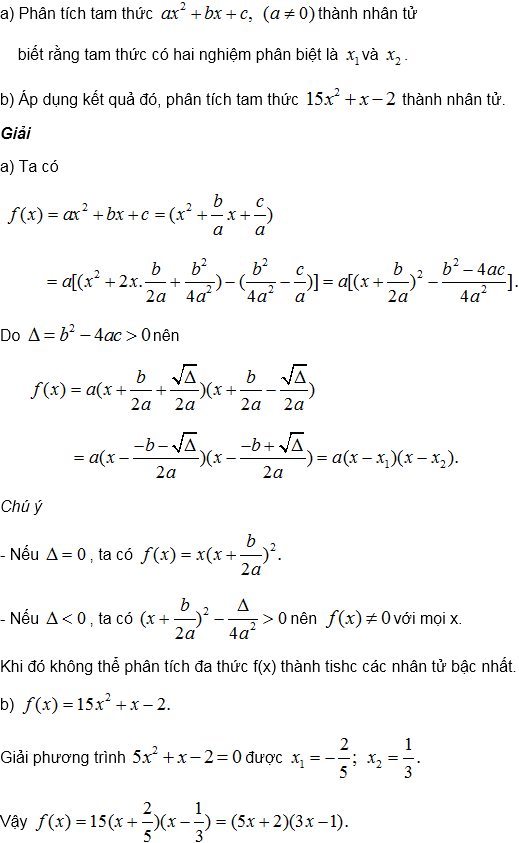
III . Bài bác tập trường đoản cú giải vận dụng cách làm tính đelta cùng đental phẩy phương trình bậc 2

Bài 1: minh chứng rằng phương trình sau bao gồm nghiệm với tất cả a ; b :

(a+1) x² – 2 (a + b)x + (b- 1) = 0

Bài 2: giả sử phương trình bậc hai x² + ax + b + 1 = 0 gồm hai nghiệm dương. Chứng tỏ rằng a² + b² là 1 hợp số.

Bài 3: mang đến phương trình (2m – 1)x² – 2(m + 4 )x +5m + 2 = 0 (m #½)

Bài 4: cho phương trình x² – 6x + m = 0. Tính cực hiếm của m, hiểu được phương trình có hai nghiệm x1, x2 vừa lòng điều khiếu nại x1 – x2 = 4.

Bài 5: cho phương trình bậc hai: 2x² + (2m – 1)x +m – 1 =0

Bài 6. cho f(x) = x² – 2(m +2)x+ 6m +1

Bài 7: cho tam thức bậc hai f(x) = ax² + bx +c vừa lòng điều khiếu nại Ι f(x)Ι =Có bốn nghiệm phân biệt.Có tía nghiệm phân biệt.Có nhị nghiệm phân biệt.Có một nghiệm
Vô nghiệm.Trên đây là nội dung bài viết giới thiệu về phương trình bậc 2 và công thức tính delta, đenlta phẩy và các bài tập áp dụng công thức đenlta để chúng ta tham khảo với luyện tập.

Mong rằng các bạn sẽ chăm chỉ luyện tập và dành được hiệu quả cao trong tiếp thu kiến thức và thi cử nhé. Mọi nỗ lực của các bạn sẽ được đền rồng đáp xứng danh nếu như bạn cần mẫn và đề nghị mẫn. Chúc các bạn thành công !

Cách tính delta, delta phẩy vào phương trình bậc 2 là một kiến thức quan trọng và là nền tảng cho các bài toán tự cơ phiên bản đến nâng cấp của toán lớp 9. Trong nội dung bài viết này, Verba
Learn sẽ trình bày đến chúng ta chi tiết cách làm tính delta, delta phẩy vận dụng giải phương trình bậc 2 cùng hàng loạt những bài tập chủng loại vận dụng.

Giới thiệu về phương trình bậc 2

Phương trình bậc 2 là phương trình bao gồm dạng: ax² + bx + c = 0

→ trong những số ấy a # 0, a, b là hệ số, c là hằng số

Công thức nghiệm phương trình bậc 2

Để giải phương trình bậc 2 cơ bản, họ sử dụng 2 công thức nghiệm delta và delta phẩy. Để áp dụng giải các bài toán biện luận nghiệm, ta sử dụng định lý Vi-et.

Công thức tính delta

Ta xét phương trình: ax² + bx +c = 0, cùng với biệt thức delta: Δ = b² – 4ac. Sẽ sở hữu 3 trường hợp:

– nếu Δ 0 thì phương trình gồm hai nghiệm phân biệt:

Trong trường đúng theo nếu b = 2b′ thì sử dụng công thức delta phẩy dưới đây.

Công thức tính delta phẩy

Ta xét phương trình: ax² + bx +c = 0. Cùng với biệt thức delta phẩy: Δ′ = b′² – ac. Trong đó: b′ = b/2

→ công thức trên nói một cách khác là công thức nghiệm thu gọn.

Tương tự như delta thì delta phẩy bọn họ cũng tất cả 3 trường đúng theo bao gồm:

– ví như Δ′ 0 thì phương trình bao gồm hai nghiệm phân biệt:

Hệ thức Viet

Cho phương trình bậc 2 một ẩn: ax2 + bx + c = 0 (a≠0) (*) gồm 2 nghiệm x1 với x2. Lúc đó 2 nghiệm này vừa lòng hệ thức sau: thì ta gồm Công thức Vi-et như sau:

Hệ thức Viet dùng để giải quyết các dạng bài bác tập không giống nhau liên quan mang lại hàm số bậc 2 và các bài toán quy về hàm số bậc 2. Xong xuôi 3 bí quyết nghiệm bên trên thì chúng ta đã có thể thoải mái làm bài tập rồi. Hãy thuộc đến các bài tập áp dụng ngay dưới đây.

Phân dạng bài tập

Ứng cùng với 3 phương pháp trên, chúng ta có những dạng bài tập tương ứng: Giải phương trình bậc 2 một ẩn cơ phiên bản và biện luận nghiệm phương trình bậc 2 một ẩn. Để giải các dạng bài bác tập này, bọn họ cần nắm rõ công thức nghiệm delta, cách làm nghiệm delta phẩy và định lý Vi-et (dùng nhằm giải các bài toán biện luận tham số).

Dạng 1. Ko dùng bí quyết nghiệm, giải phương trình bậc nhì một ẩn cho trước

Cách giải: Ta hoàn toàn có thể sử dụng một trong những cách sau

Cách 1: Đưa phương trình đã mang lại về dạng tích

Cách 2: Đưa phương trình đã mang lại về phương trình cơ mà vế trái là 1 bình phương còn vế phải là một hằng số.

Câu 1. Giải các phương trình sau

a) 5x2 – 7x = 0

b) –3x2 + 9 = 0

c) x2 – 6x + 5 = 0

d) 3x2 + 12x + 1 = 0

Hướng dẫn giải

a) Ta có: 5x2 – 7x = 0

⇔ x(5x – 7) = 0

⇔ x ∈

b) Ta có: –3x2 + 9 = 0

⇔ 3x2 – 9 = 0

⇔ 3(x2 – 3) = 0

⇔ x ∈

c) Ta có: x2 – 6x + 5 = 0

⇔ (x – 1)(x – 5) = 0

⇔ x ∈ 1; 5

d) Ta có: 3x2 + 12x + 1 = 0

⇔ 3(x + 2)2 = 11

⇔ x =

Câu 2. Giải các phương trình sau

a) " />

b) " />

c) x2 – x – 9 = 0

d) 3x2 + 6x + 5 = 0

Hướng dẫn giải

a) Ta có: " />

b) Ta có: " />

c) Ta có: x2 – x – 9 = 0

⇔ x ∈

d) Ta có:

Vậy phương trình vô nghiệm.

Câu 3. Giải các phương trình sau

a) " />

b) (m2 + 2)x2 – 5 = 0 với m ∈ ℝ

c)

d) x2 – 3x + 2 = 0

Hướng dẫn giải

a) Ta có: " />

Vậy tập nghiệm của phương trình là

b) Ta có:

Vậy tập nghiệm của phương trình là

c) Ta tất cả :

Vậy tập nghiệm của phương trình là

d) Ta có: x2 – 3x + 2 = 0

⇔ x2 – x – 2x + 2 = 0

⇔ (x – 1)(x – 2) = 0

⇔ x = 1 ∨ x = 2

Vậy tập nghiệm của phương trình là S = 1; 2.

Câu 4. với cái giá trị như thế nào của thông số m thì phương trình 4x2 + m2x + 4m = 0 tất cả nghiệm x = 1

Hướng dẫn giải

Thay x = 1 vào phương trình ta có:

4⋅12 + m2⋅1 + 4m = 0 ⇔ m = –2

Vậy m = −2

Câu 5. đến phương trình 4mx2 – x – 10m2 = 0. Tìm những giá trị của thông số m để phương trình gồm nghiệm x = 2

Hướng dẫn giải

Thay x = 2 vào phương trình ta được:

4m⋅22 – 2 – 10m2 = 0

⇔ –10m2 + 16m – 2 = 0

⇔ m =

Câu 6. đến phương trình x2 – (2m + 1)x + m2 – 2m + 3 = 0 (1). Giải phương trình (1) biết phương trình (1) bao gồm một nghiệm x = 2.

Hướng dẫn giải

Vì phương trình gồm nghiệm x = 2 phải ta có:

22 – (2m + 1)⋅2 + mét vuông – 2m + 3 = 0

⇔ 4 – 4m – 2 + m2 – 2m + 3 = 0

⇔ m2 – 6m + 5 = 0

⇔ m ∈ 1; 5

– m = 1 ⇒ x2 – 3x + 2 = 0 ⇔ x ∈ 1; 2

– m = 5 ⇒ x2 – 11x + 18 = 0 ⇔ x ∈ 9; 2

Dạng 2. Giải phương trình bậc hai bằng phương pháp sử dụng phương pháp nghiệm, công thức nghiệm thu sát hoạch gọn

Sử dụng bí quyết nghiệm, công thức sát hoạch gọn của phương trình bậc hai nhằm giải.

Câu 1. xác minh hệ số a, b, c; Tính biệt thức ∆ (hoặc ∆’ ví như b = 2b’) rồi tra cứu nghiệm của những phương trình sau

a) 2x2 – 3x – 5 = 0

b) 2x2 – 6x + 8 = 0

c) 9x2 – 12x + 4 = 0

d) –3x2 + 4x – 4 = 0

Hướng dẫn giải

a) Ta có: x = 2; b = –3; c = –5 và ∆ = 49 > 0 ⇒ phương trình gồm hai nghiệm phân biệt:

b) Ta có: a = 1; b = –6; b’ = –3; c = 8; ∆’ = 1 > 0 ⇒ x ∈ 2; 4

c) Ta có: a = 9; b = –12; c = 4; ∆ = 0 ⇒ phương trình tất cả nghiệm kép: x1 = x2 =

d) Ta có: a = –3; b = 4; c = –4; ∆ = –32 ⇒ phương trình vô nghiệm.

Câu 2. khẳng định hệ số a, b, c; Tính biệt thức ∆ (hoặc ∆’ trường hợp b = 2b’) rồi tìm nghiệm của những phương trình sau

a) x2 – x – 11 = 0

b) x2 – 4x + 4 = 0

c) –5x2 – 4x + 1 = 0

d) –2x2 + x – 3 = 0

Hướng dẫn giải

a) Ta có: a = 1; b = –1; c = –11; ∆ = 45 > 0 ⇒ x ∈

b) Ta có: a = 1; b = –4; c = 4; ∆ = 0 ⇒ x = 2

c) Ta có: a = –5; b = –4; c = 1; ∆ = 36 > 0 ⇒ x ∈

d) Ta có: a = –2; b = 1; c = –3; ∆ = –23

b) Ta có:

c) Ta có:

d) Ta có:

Câu 4. Giải những phương trình sau

a)

b) 152x2 – 5x + 1 = 0

c)

d)

Hướng dẫn giải

a) Ta có:

b) Ta có: a = 152; b = –5; c = 1; ∆ = –583 2 – (5 – m)x + 2 – m = 0 cùng với m ∈ ℝ là tham số

a) xác minh các thông số a, b, c của phương trình.

b) Giải phương trình trong số trường hợp mm = 2; m = 5; m = 1.

Hướng dẫn giải

a) Ta có: a = 3; b = –(5 – m); c = 2 – m

b) với m = 5 ta tất cả phương trình:

3x2 – 3 = 0 ⇔ x2 = 1 ⇔ x = ±1

Với m = 2 ta có phương trình:

3x2 – 3x = 0 ⇔ 3x(x – 1) = 0 ⇔ x = 0 ∨ x = 1

Với m = 1 ta bao gồm phương trình:

3x2 – 4x + 1 = 0

⇔ 3x2 – 3x – x + 1 = 0

⇔ (3x – 1)(x – 1) = 0

⇔ x =

Nhận xét: vào cả 3 trường hợp phương trình đều phải có nghiệm x = 1

Ta có thể biến đổi phương trình ban sơ tương đương với

Dạng 3. Thực hiện công thức nghiệm, khẳng định số nghiệm của phương trình dạng bậc hai

Cách giải: Xét phương trình bậc hai: ax2 + bx + c = 0

– Phương trình tất cả nghiệm kép

– Phương trình bao gồm hai nghiệm sáng tỏ

– Phương trình bao gồm đúng một nghiệm

– Phương trình vô nghiệm

Hướng dẫn giải

Ta có: ∆’ = 4m2 – 4m – 24

Phương trình (1) bao gồm nghiệm kép ⇔ ∆’ = 0

⇔ 4m2 – 4m – 24 = 0

⇔ mét vuông – m – 6 = 0

⇔ m = –2 ∨ m = 3

Vậy m ∈–2; 3.

Câu 2. đến phương trình mx2 + (2m – 5)x + m – 2 = 0 (1) cùng với m ∈ ℝ là tham số. Lúc nào

a) Phương trình (1) có nghiệm

b) Phương trình (1) có hai nghiệm phân biệt

Hướng dẫn giải

Xét 2 tường hợp

TH1: với m = 0 phương trình thay đổi –5x – 2 = 0 ⇔ x =

TH2: với m ≠ 0 phương trình mx2 + (2m – 5)x + m – 2 = 0 là 1 trong những phương trình bậc hai và có

∆ = (2m – 5)2 – 4m(m – 2) = –12m + 25

– nếu ∆ = –12m + 25 > 0 ⇔ m 1 = x2

Vậy:

a) Phương trình (1) bao gồm nghiệm khi và chỉ còn khi m ≤

b) Phương trình (1) tất cả hai nghiệm tách biệt khi và chỉ khi m ≠ 0 và m 2 – 2(m – 2)x – 1 = 0 với m là tham số.

a) Giải phương trình cùng với m = 2

b) minh chứng rằng với mọi m ∈ ℝ, phương trình luôn có nghiệm. Với giá trị làm sao của m thì phương trình tất cả hai nghiệm phân biệt.

Hướng dẫn giải

a) với m = 2, phương trình đang cho biến x2 – 1 = 0 ⇔ x = ±1

b) Xét nhị trường hợp

TH1: với m = " /> phương trình vẫn cho biến chuyển x – 1 = 0 ⇔ x = 1

TH2: với m ≠ " /> phương trình (2m – 3)x2 – 2(m – 2)x – 1 = 0 là 1 phương trình bậc hai cùng có

∆’ = (m – 2)2 + (2m + 3) = (m – 1)2 ≥ 0, ∀m ∈ ℝ

Suy ra phương trình luôn có nghiệm với mọi m ∈ ℝ

Phương trình bao gồm hai nghiệm tách biệt khi và chỉ còn khi

Cách khác:

(2m – 3)x2 – 2(m – 2)x – 1 = 0

⇔ (2m – 3)x2 – (2m – 3)x + x – 1 = 0

⇔ (x – 1)<(2m – 3)x + 1> = 0

⇔

Suy ra phương trình luôn có nghiệm x = 1 với đa số m ∈ ℝ.

Phương trình gồm hai nghiệm phân minh khi và chỉ khi phương trình (2m – 3)x + 1 gồm nghiệm khác 1

Câu 4. mang đến phương trình mx2 – 2(m – 1)x + m – 3 = 0 (m là tham số). Tìm các giá trị của m để phương trình

a) có hai nghiệm phân biệt

b) bao gồm nghiệm kép

c) Vô nghiệm

d) tất cả đúng một nghiệm

e) gồm nghiệm

Hướng dẫn giải

Ta có: ∆’ = (m – 1)2 – m(m – 3) = m + 1

a) Phương trình gồm hai nghiệm phân biệt

b) Xét m ≠ 0. Phương trình có nghiệm kép khi

c) Ta tìm kiếm được m 2 – 2(m + 1)x + m = 0 (m là tham số). Tìm những giá trị của m để phương trình

a) tất cả hai nghiệm phân biệt

b) gồm nghiệm kép

c) Vô nghiệm

d) bao gồm đúng một nghiệm

e) bao gồm nghiệm

Hướng dẫn giải

Ta có: ∆’ = (m + 1)2 – m(m – 2) = 4m + 1

a) Phương trình gồm hai nghiệm phân biệt

b) kiếm được

c) Ta kiếm được

Hướng dẫn giải

Đặt x2 + 2x – 2m + 7 = 0 là phương trình (1)

x2 + 6x + mét vuông + 6 = 0 là phương trình (2)

Ta có: ∆’1 = 1 + 2m – 7 = 2m – 6 với ∆’2 = 32 – (m2 + 6) = 3 – m2

Suy ra: ∆’1 + ∆’2

= 2m – 6 + 3 – m2

= –(m2 – 2m + 1) – 2

= –(m – 1)2 – 2 1 với ∆’2 có tối thiểu một số nhỏ hơn 0 (đpcm).

Câu 7. với cái giá trị như thế nào của m, hai phương trình sau tất cả nghiệm chung

(1) 2x2 – (3m + 2)x + 12 = 0 và (2) 4x2 – (9m – 2)x + 36 = 0

Hướng dẫn giải

Gọi x0 là một trong những nghiệm bình thường của nhì phương trình, ta có:

– trường hợp –3m + 6 = 0 ⇔ m = 2 thì phương trình (*) vô nghiệm

– nếu như –3m + 6 ≠ 0 ⇔ m ≠ 2 thì phương trình (*) có một nghiệm

Thay vào phương trình (1) ta có:

Vậy cùng với m = 3 nhị phương trình sẽ cho có một nghiệm bình thường x0 = 4.

Câu 8. cho phương trình x2 + (m – 5)x – 3(m – 2) = 0 với m ∈ ℝ là tham số

a) chứng tỏ rằng phương trình trên luôn luôn có nghiệm x = 3 với đa số m ∈ ℝ

b) search m nhằm phương trình gồm nghiệm kép

c) search m để phương trình gồm hai nghiệm minh bạch x1, x2 thỏa mãn x1 = 3x2

Hướng dẫn giải

a) Ta có: x2 + (m – 5)x – 3(m – 2) = 0

⇔ x2 – 3x + (m – 2)x – 3(m – 2) = 0

⇔ x(x – 3) + (m – 2)(x – 3) = 0

⇔ (x – 3)(x + m – 2) = 0

⇔ x = 3 ∨ x = 2 – m

Vậy phương trình trên luôn có nghiệm x = 3 với tất cả m ∈ ℝ

b) Phương trình bao gồm nghiệm kép khi còn chỉ khi nhị nghiệm của phương trình trùng nhau

Theo câu a) suy ra: 2 – m = 3 ⇒ m = –1

Ta cũng rất có thể xét:

∆ = (m – 5)2 + 4⋅3(m – 2)

= m2 + 2m + 1 = (m + 1)2

Phương trình tất cả nghiệm kép ⇔ ∆ = 0 ⇔ (m + 1)2 = 0 ⇔ m = –1

c) Xét 2 ngôi trường hợp

TH1: x1 = 3 với x2 = 2 – m

Khi đó: x1 = 3x2 ⇔ 3 = 3(2 – m) ⇔ 2 – m = 1 ⇔ m = 1

TH2: x1 = −2 và x2 = 3

Khi đó: x1 = 3x2 ⇔ 2 – m = 3m ⇔ 4m = 2 ⇔ m = " />

Câu 9. Cho Parabol (P): y = 4x2 và đường thẳng d: y = 2mx – 1 cùng với m ∈ ℝ là tham số. Tìm m để:

a) Đường thẳng d cắt parabol (P) tại hai điểm phân biệt

b) Đường trực tiếp d là tiếp tuyến đường của parabol (P)

Hướng dẫn giải

Phương trình hoành độ giao điểm của (P) và d là:

4x2 = 2mx + 1 ⇔ 4x2 – 2mx – 1 = 0 (1)

a) Đường thẳng d giảm (P) tại 2 điểm phân minh khi và chỉ khi phương trình (1) tất cả hai nghiệm phân minh ⇔ ∆’ > 0 ⇔ mét vuông – 4 > 0 ⇔ m2 > 4 ⇔ |m| > 2 ⇔ m > 2 ∨ m 2 hoặc m 2 – 4 = 0 ⇔ m = ±2

Khi đó ta gồm đường thẳng y = 4m – 1 cùng y = –4m – một là các tiếp con đường của Parabol (P).

Xem thêm: Khám Phá Nơi Tận Cùng Thế Giới Hd Vietsub, Khám Phá Nơi Tận Cùng Thế Giới

Câu 10. đến phương trình: mx2 – (2m + 1)x + m + 1 = 0

a) chứng minh rằng phương trình luôn luôn có nghiệm cùng với ∀m ∈ ℝ

b) tìm kiếm m để phương trình (1) có 1 nghiệm to hơn 2

Hướng dẫn giải

a)

– m = 0 ⇒ x = 1

– m ≠ 0 ⇒ ∆ = 1 > 0 ⇒ (1) luôn có nghiệm ∀m ∈ ℝ

b) cùng với m = 0 thì phương trình (1) có một nghiệm x = 1

Vậy 0 cách thức giải

Cách giải:

Giải với biện luận phương trình dạng bậc nhị theo tham số m là tra cứu tập nghiệm của phương trình phụ thuộc vào sự chuyển đổi của m.

Xét phương trình bậc hai dạng: ax2 + bx + c = 0 cùng với ∆ = b2 – 4ac (hoặc ∆’ = b’2 – ac).

– giả dụ a = 0, ta đem về biện luận phương trình bậc nhất

– nếu a ≠ 0, ta biện luận phương trình bậc nhì theo ∆.

Câu 1. Giải và biện luận phương trình

(m – 2)x2 – (2m – 1)x + m + 2 = 0

Hướng dẫn giải

– m = 2 ⇒ x = " />

– m ≠ 2 ⇒ ∆ = –4m + 17

m > " /> → ∆ 0 → (1) có hai nghiệm phân biệt:

Vậy m = 2 phương trình có nghiệm x = " />

m > " /> ⇒ phương trình vô nghiệm

m = " /> ⇒ phương trình tất cả nghiệm kép x =

m 2 – 2mx + m + 1 = 0 (m là tham số)

a) Giải phương trình lúc m = –2

b) Giải cùng biện luận phương trình theo m

Hướng dẫn giải

a)

b) Ta xét nhì trường đúng theo sau:

TH1: m = 0 ⇒ 1 = 0 (vô nghiệm)

TH2: m ≠ 0 ⇒ ∆’ = –m ≠ 0

– m 0 ⇒

– m > 0 ⇒ ∆’ 2 + (1 – m)x – m = 0

b) (m – 3)x2 – 2mx + m – 6 = 0

Hướng dẫn giải

a) Ta có: ∆ = mét vuông + 2m + 1 =(m + 1)2 ≥ 0, ∀m ⇒

– ∆ = 0 ⇔ m = –1: m Phương trình đã cho gồm nghiệm kép:

– ∆ > 0 ⇔ m ≠ –1: m Phương trình đã cho bao gồm hai nghiệm phân biệt: x1 = m; x2 = –1

b) với m = 3 ⇒ Phương trình gồm dạng: –6x – 3 = 0 ⇔ x =

Với m ≠ 3 ⇒ ∆’ = 9m – 18

– ∆’ 0 ⇔

Câu 4. Giải với biện luận những phương trình sau (m là tham số)

a) mx2 + (2m – 1)x + m + 2 = 0

b) (m – 2)x2 – 2(m + 1)x + m = 0

Hướng dẫn giải

a) cùng với m = 0 ⇒ x = 2

Với m ≠ 0 ⇒ ∆ = –12m + 1

– ∆ : Phương trình vô nghiệm

– ∆ = 0 ⇔

– ∆ > 0 ⇔

Dạng 5. Dạng toán tương quan đến tính có nghiệm của phương trình bậc hai, nghiệm thông thường của phương trình bậc hai

Cách giải:

– Phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0) gồm nghiệm ⇔ ∆ ≥ 0 (hoặc ∆’ ≥ 0 ).

– mong tìm đk của tham số để hai phương trình dạng bậc nhị ax2 + bx + c = 0 với a’x2 + b’x + c’ = 0 bao gồm nghiệm tầm thường ta có tác dụng như sau:

Bước 1: gọi x0 là nghiệm bình thường của hai phương trình. Cố kỉnh x0 vào 2 phương trình để kiếm được điều kiện của tham số.

Bước 2: với mức giá trị của thông số vừa kiếm tìm được, thay quay trở về để chất vấn xem 2 phương trình có nghiệm chung hay không và kết luận.

– muốn tìm đk của tham số nhằm hai phương trình dạng bậc nhì ax2 + bx + c = 0 và a’x2 + b’x + c’ = 0 tương đương, ta xét nhì trường hợp:

Trường phù hợp 1: hai phương trình thuộc vô nghiệm

Trường thích hợp 2: nhì phương trình cùng có nghiệm. Lúc đó:

– Điều kiện đề nghị để nhì phương trình tương tự là chúng có nghiệm chung. Từ đó kiếm được điều khiếu nại của tham số

– Điều kiện đủ với mức giá trị của tham số vừa kiếm tìm được, thay quay trở lại để khám nghiệm xem 2 phương trình tập nghiệm đều bằng nhau không với kết luận.

Câu 1. đến hai phương trình:

x2 + x + a = 0; x2 + ax + 1 = 0

a) search a nhằm hai phương trình có nghiệm chung

b) tìm kiếm a để hai phương trình tương đương

Hướng dẫn giải

a) trả sử x0 là nghiệm thông thường của nhì phương trình → ta tất cả hệ:

– với a = 1 ⇒ x2 + x + 1 = 0 (vô nghiệm)

– x0 = 1 ⇒ (1): a = –2

Vậy cùng với a = –2 thì nhì phương trình có nghiệm phổ biến x = 1.

b) Theo câu a hai phương trình gồm tập nghiệm khác nhau. Vậy để chúng tương đương khi còn chỉ khi chúng cùng vô nghiệm

(n – b)2 = (m – a)(an – bm) (1)

Hướng dẫn giải

Giả sử x0 là nghiệm phổ biến của hai phương trình → ta có hệ:

– a – m = 0 ⇔ a = m ⇒ (*) ⇒ n = b ⇒ (1) đúng

– a ≠ m ⇒ (*) ⇒

Câu 3. tìm kiếm m để hai phương trình: x2 – (2m – 3)x + 6 = 0; 2x2 + x + m – 5 = 0 bao gồm duy độc nhất nghiệm chung.

Hướng dẫn giải

Giả sử x0 là nghiệm bình thường của hai phương trình → ta gồm hệ:

– m = −1 nhị phương trình ban đầu trở thành:

x2 + 5x + 6 = 0; 2x2 + x – 6 = 0

Hai phương trình này có nghiệm chung x = –2. Vậy m = –1 là giá chỉ trị đề nghị tìm.

Câu 4. đến a, b, c là ba cạnh của một tam giác. Chứng minh phương trình b2x2 – (b2 + c2 – a2)x + c2 = 0 luôn vô nghiệm.

Hướng dẫn giải

Ta có: ∆ = (b – c – a)(b – c + a)(b + c – a)(b + c + a)

Vì a, b, c là bố cạnh của một tam giác nên:

b – c – a 0; b – c + a > 0; b + c + a > 0 ⇒ ∆ 2 + (a + b + c)x + (ab + bc + ca) = 0 cùng với a, b, c là tía cạnh của một tam giác. Chứng minh phương trình trên luôn vô nghiệm.

Hướng dẫn giải

Ta có: ∆ = a2 + b2 + c2 – 2ab – 2bc – 2ca

Vì a 2 2 2 2 + ax + b = 0; x2 + cx + d = 0. Chứng minh nếu hai phương trình trên bao gồm nghiệm phổ biến thì: (b – d)2 + (a – c)(ad – bc) = 0.

Hướng dẫn giải

Gọi x0 là nghiệm bình thường của nhì phương trình. Ta có: (a – c)x0 = d – b

– nếu

– ví như a = c ⇒ b = d ⇒ đpcm.

Câu 7. mang đến hai phương trình x2 + ax + b = 0 và x2 + bx + a = 0 trong các số đó

Hướng dẫn giải

Ta có: ∆1 + ∆2 = a2 + b2 – 4(a + b)

Từ

⇒ đpcm.

Câu 8. mang đến hai phương trình x2 + x – m = 0 cùng x2 – mx + 1 = 0. Tìm các giá trị của tham số m để:

a) nhì phương trình có nghiệm chung

b) nhị phương trình tương đương

Hướng dẫn giải

a) call x0 là nghiệm bình thường của nhì phương trình.

Ta biến hóa được (1 + m)x0 = m + 1.

Tìm được m = −1 hoặc m = 2

b) Ta xét 2 trường hợp:

Trường phù hợp 1: nhì phương trình cùng vô nghiệm

a) hai phương trình gồm nghiệm chung

b) nhì phương trình bên trên tương đương

Hướng dẫn giải

a) Ta tìm được a ∈ ∅

b) tìm kiếm được

Nếu có một số thực m làm thế nào cho a⋅f(m) 0 hfill \ endgathered > " />

Câu 1. chứng tỏ rằng với ∀m những phương trình sau luôn luôn có nghiệm:

a) x2 – 2(m + 2)x – m – 7 = 0

b) x2 – 4m2x – 4m – 2 = 0

Hướng dẫn giải

a) Ta có:

Vậy phương trình đã cho luôn luôn có hai nghiệm phân biệt với đa số m.

b) Ta có: ∆’ = 4m4 + 4m + 2 = 2(2m4 + 2m + 1). Mà:

Dấu “=” xẩy ra

Vậy phương trình luôn luôn có nhị nghiệm phân biệt.

Câu 2. chứng tỏ rằng nếu như a, b, c là độ dài các cạnh của 1 tam giác thì phương trình sau vô nghiệm: a2x2 + (a2 + b2 + c2)x + b2 = 0

Hướng dẫn giải

Ta có: a2 ≠ 0

⇒ ∆ 2 + (a + b)2 + a(c + 2) + 1 2 + bx + c = 0 luôn luôn có nhì nghiệm phân biệt.

Hướng dẫn giải

Phân tích:

Vì câu hỏi yêu cầu minh chứng phương trình gồm hai nghiệm phân biệt đề nghị phương trình sẽ cho yêu cầu là phương trình bậc hai, có nghĩa là a ≠ 0. Điều này dễ dàng thấy luôn đúng, vị nếu a = 0 thì từ đưa thiết ta gồm b2 + 1 2 – 4ac > 0 hoặc đã cho thấy số thực m làm sao cho a⋅f(m) 2 + bx + c.

Cách 1: Để minh chứng ∆ = b2 – 4ac > 0, ta thay đổi giả thiết việc như sau:

16a2 + 4(a + b)2 + 4ac + 8a + 4 2 – 4ac > 16a2 + 4(a + b)2 + 4ac + 8a + 4

⇔ b2 – 4ac > 12a2 + 4(a + b)2 + b2 + 4(a + 1)2 ≥ 0

⇒ ∆ = b2 – 4ac > 0

Vậy phương trình đã cho luôn luôn có nhị nghiệm phân biệt

Cách 2: Để chỉ ra có một vài thực m sao để cho a⋅f(m) = a(am2 + bm + c) 2 + a2 + 2ab + b2 + ac + 2a + 1 2 – b2 ≤ 0

⇔ a(4a + 2b +c) 2 + bx + c = 0 luôn có nghiệm.

Hướng dẫn giải

Phương trình vẫn cho chưa hẳn là phương trình bậc hai vì ta chưa biết a = 0 hay a ≠ 0. Vì vậy ta xét những trường hòa hợp sau:

– Xét a = 0, khi đó:

b = 0, từ mang thiết bao gồm c = 0. Vị đó, phương trình đang cho gồm vô số nghiệm

b ≠ 0 thì phương trình vẫn cho bao gồm nghiệm

– Xét a ≠ 0, lúc đó phương trình đã cho rằng phương trình bậc hai. Để chứng tỏ phương trình gồm nghiệm, ta gồm thể minh chứng ∆ = b2 – 4ac ≥ 0 hoặc đã cho thấy số thực m vừa lòng a⋅f(m) 2 + bx + c.

Cách 1: Để minh chứng ∆ = b2 – 4ac ≥ 0 ta đổi khác như sau:

Ta có:

Vì 9a2 – 10ac + 225c2

= 25c2 – 10ac + a2 + 8a2 + 200c2

= (5c – a)2 + 8a2 + 200c2 ≥ 0

⇒ ∆ ≥ 0 với tất cả a, b, c. Vậy phương trình vẫn cho luôn luôn có nghiệm.

Cách 2: Để đã cho thấy số thực m vừa lòng a⋅f(m) 2 + bx + c tất cả nghiệm, ta có thể chứng tỏ như sau

Cách 1: chứng tỏ ∆ = b2 – 4ac ≥ 0 (khi a ≠ 0 )

Cách 2: đã cho thấy tồn trên x, y, z thỏa mãn: x⋅f(α) + y⋅f(β) + z⋅f(γ) = ma + nb + pc lúc ấy trong ba số f(α), f(β), f(γ) luôn có nhì số trái dấu. Từ đó ta bao gồm đpcm.

Câu 5. cho các sô a, b, c thỏa mãn a + 2b + 3c = 1. Minh chứng rằng ít nhất 1 trong các hai phương trình sau gồm nghiệm: 4x2 – 4(2a + 1)x + 4a2 + 192abc + 1 = 0 và 4x2 – 4(2b + 1)x + 4b2 + 96abc + 1 = 0

Hướng dẫn giải

Hai phương trình trên lần lượt gồm ∆’1 = 16a(1 – 48bc); ∆’2 = 16(1 – 24ac). Do a, b là những số dương buộc phải ∆’1, ∆’2 lần lượt cùng dấu với cùng một – 48bc và 1 – 24ac. Để minh chứng bài toán, ta cần minh chứng trong hai biệt thức ∆’1, ∆’2 luôn có ít nhất một trong những không âm. Để chứng tỏ điều này, ta đi xét tổng ∆’1 + ∆’2. Trường hợp ∆’1 + ∆’2 ≥ 0 thì trong hai số ∆’1, ∆’2 có ít nhất một trong những không âm. Ta có:

1 – 48bc + 1 – 24ac

= 2 – 24c(a + 2b)

= 2 – 24c(1 – 3c)

= 2(6c – 1)2 ≥ 0

Hay ∆’1 + ∆’2 ≥ 0

Vậy gồm ít nhất 1 trong những hai phương trình trên tất cả nghiệm.

Câu 6. đến phương trình ax2 + bcx + b3 + c3 – 4abc = 0 (1) (a ≠ 0) vô nghiệm. Minh chứng rằng trong hai phương trình sau có 1 phương trình vô nghiệm, 1 phương trình gồm hai nghiệm phân biệt: ax2 + bx + c = 0 (2); ax2 + cx + b = 0 (3).

Hướng dẫn giải

Phương trình (1) vô nghiệm

⇒ ∆1 = b2c2 – 4a( b3 + c3 – 4abc) 2 = b2 – 4ac; ∆3 = c2 – 4ab

Ta đi minh chứng ∆2⋅∆3 0 hfill \ endgathered ight. hfill \ endgathered ight. Rightarrow lap-- Dpcm> " />

Câu 7. mang đến a, b, c là những số thực gồm tổng khác 0. Minh chứng rằng phương trình sau luôn luôn có nghiệm:

a(x – b)(x – c) + b(x – c)(x – a) + c(x – a)(x – b) = 0 (1)

Hướng dẫn giải

(1) ⇔ (a + b + c)x2 – 2(ab + bc + ca)x + 3abc = 0

∆’ = (ab + bc + ca)2 – 3abc(a + b + c)

= a2b2 + b2c2 + c2a2 – abc(a + b + c)

= " /> <(ab – bc)2 + (bc – ca)2 + (ca – ab)2> ≥ 0

⇒ đpcm

Câu 8. cho các số a, b, c thỏa mãn a + b + c = 6. Chứng minh rằng bao gồm ít nhất 1 trong những ba phương trình sau tất cả nghiệm: x2 + ax + 1 = 0; x2 + bx + 1 = 0; x2 + cx + 1 = 0

Hướng dẫn giải

Câu 9. Cho phương trình ax2 + bcx + b3 + c3 – 4abc = 0 (1) (a ≠ 0) vô nghiệm. Minh chứng rằng trong nhì phương trình sau gồm một phương trình vô nghiệm cùng một phương trình có hai nghiệm tách biệt ax2 + bx + c = 0 (2); ax2 + cx + d = 0 (3)

Hướng dẫn giải

Vì phương trình (1) vô nghiệm đề nghị ta có: ∆1 = b2c2 – 4a(b3 + c3 – 4abc) 2 = b2 – 4ac; ∆3 = c2 – 4ab

Để chứng minh bài toán ta cần minh chứng trong nhì số ∆2, ∆3 luôn luôn có một trong những âm và một số trong những dương.

Điều này gợi ý ta đi minh chứng ∆2⋅∆3 2 – 4ac)(c2 – 4ab) 2⋅∆3 2, ∆3 có một trong những âm và một trong những dương dẫn mang đến trong nhì phương trình (2), (3) luôn có một phương trình bao gồm hai nghiệm tách biệt và một phương trình vô nghiệm.

Bài tập từ bỏ luyện

Câu 1. Giải các phương trình sau

a)

b) 3x2 + 3 = 2(x + 1)

c)

d)

Hướng dẫn giải

a) Ta tìm được:

b) Ta tìm được: x ∈ ∅

c) Ta kiếm tìm được:

d) Ta tìm được:

Câu 2. cho phương trình 2x2 – (4m + 3)x + 2m2 – 1 = 0 (m là tham số). Tìm các giá trị của m nhằm phương trình:

a) bao gồm hai nghiệm phân biệt

b) gồm nghiệm kép

c) Vô nghiệm

d) gồm đúng một nghiệm

e) gồm nghiệm

Hướng dẫn giải

Ta có: ∆ = (4m + 3)2 – 4⋅2(2m2 – 1)

= 16m2 + 24m + 9 – 16m2 + 8

= 24m + 7

a) Phương trình có hai nghiệm phân minh khi m > " />

b) Phương trình tất cả nghiệm kép lúc m = " />

c) Phương trình vô nghiệm khi m 2 – 4(m – 1)x + 4m + 8 = 0 (m là tham số).

Hướng dẫn giải

Ta chia ra làm những trường đúng theo sau:

– m ≠ 0; m > –1

– m = –1

– m 2 + mx + 2 = 0 cùng x2 + 2x + m = 0. Khẳng định các cực hiếm của tham số m để hai phương trình:

a) gồm nghiệm chung

b) Tương đương

Hướng dẫn giải

a) Ta kiếm được m = 2 hoặc m = −3

b) Ta tìm được

Câu 1. đến phương trình x² – 2(m+1)x + m² + m +1 = 0

Tìm các giá trị của m để phương trình bao gồm nghiệm

Trong trường hợp phương trình tất cả nghiệm là x1, x2 hãy tính theo m

Câu 2. chứng tỏ rằng phương trình sau có nghiệm với mọi a, b:

(a+1) x² – 2 (a + b)x + (b- 1) = 0

Câu 3. đưa sử phương trình bậc nhị x² + ax + b + 1 = 0 gồm hai nghiệm dương. Minh chứng rằng a² + b² là 1 trong những hợp số.

Câu 4. mang lại phương trình (2m – 1)x² – 2(m + 4 )x +5m + 2 = 0 (m #½)

Tìm quý giá của m để phương trình gồm nghiệm.

Khi phương trình gồm nghiệm x1, x2, hãy tính tổng S với tích p. Của hai nghiệm theo m.

Tìm hệ thức giữa S cùng P làm thế nào để cho trong hệ thức này không tồn tại m.

Câu 5. đến phương trình x² – 6x + m = 0. Tính cực hiếm của m, biết rằng phương trình tất cả hai nghiệm x1, x2 thỏa mãn điều kiện x1 – x2 = 4.